Arties: Meta-Design
as Evolving Colonies of Artistic Agents
R. Neal Elzenga, Michael S. Pontecorvo.
Emergent
Design, San Francisco, USA.
e-mail: ponte@emergent-design.com
Abstract
Meta-design, the act of designing a system or species of design instead of a design instance, is an important concept in modern design practice and in the generative design paradigm. For meta-design to be a useful tool, the designer must have more formal support for both design species definition/expression and the abstract attributes which the designer is attempting to embody within a design. Arties is an exploration of one possible avenue for supporting meta-design.
Arties is an artistic system emphasising
the co-evolution of colonies of Artificial Life design or artistic agents (called
arties) and the environment they inhabit.
Generative design systems have concentrated on biological genetics
metaphors where a population of design instances are evolved directly from a
set of ‘parent’ designs in a succession of generations. In Arties, the a-life
agent which is evolved, produces the design instance as a by-product of
interacting with its environment.
Arties utilise an attraction potential
curve as their primary dynamic. They sense the relative attraction of entities
in their environment, using multiple sensory channels. Arties then associate an
attractiveness score to each entity. This attractiveness score is combined with
a 'taste' function built into the artie that is sensitised to that observation
channel, entity, and distance by a transfer function. Arties use this attraction to guide decisions and behaviours. A
community of arties, with independent evolving attraction criteria can pass
collective judgement on each point in an art space. As the Artie moves within
this space it modifies the environment in reaction to what it senses.
Arties support for Meta-design is in
(A) the process of evolving arties, breeding their attraction potential
curve parameters using a genetic algorithm and (B) their use of sensory
channels to support abstract attributes geometry. Adjustment of these
parameters tunes the attraction of the artie along various sensing channels.
The multi-agent co-evolution of Arties is
one approach to creating a system for supporting meta-design. Arties is part of
an on-going exploration of how to support meta-design in computer augmented
design systems.
Our future work with Arties-like systems will be concerned with applications in areas such as modelling adaptive directives in Architecture, Object Structure Design, spatio-temporal behaviours design (for games and simulations), virtual ambient spaces, and representation and computation of abstract design attributes.
1. Introduction
Arties is an experimental multi-agent environment for exploration of emergent behaviour and meta-design. Arties was originally conceived of as a set of agent tools for creating adaptive game dynamics. We are also using it as one model for meta-design.
In Arties, the emphasis is on the co-evolution of colonies of A-Life (Artificial Life) design or artistic agents and the environment they inhabit. Generative design systems for the most part have tended to concentrate on biological models involving genetic metaphors [1][2]. In these systems a population of design instances are evolved from a set of ‘parent’ designs in a succession of generations. In the Arties system we have sought to define a co-evolutionary means [3] for evolving multiple flavours of agents which generate new design/art instances as a by-product of their ‘life’ activity.
2. Arties
The Arties system
consists of a collection of software agents. These agents are called Arties. An artie is an artistic a-life agent
for exploring and modifying artistic 'spaces'.
Arties are a-life ‘beings’ that possess the following characteristics:
Situatedness
- Arties exist with an environment. The arties micro-world defines a Complex
Adaptive System (CAS) [4]. This
environment must have the following characteristics:
-
A unique co-ordinate system for locating
an artie and each object in the environment relative to the artie's co-ordinates.
- A distance metric that represents the environment geometry's direct or shortest path (used for action at-a-distance calculations). In addition, a mobile artie will be able to traverse the environment along a continuous trajectory. The environment must support this notion of a trajectory. Given two co-ordinates in the environment which satisfy the above criteria, points A and B, we have the following:
A |
coordinates (x,y,z,…) |
|
B |
coordinates (x,y,z,…) |
|
|A – B| |
distance
metric for 'straight' path (in the given geometry) between A and B |
|
Path(A,B) |
distance metric of the path an artie takes to get from A to B |
|
|A – B| / Path(A,B) |
deviation metric of
the Path(A,B) form the straight line
metric |A - B|. |
Table
2.0 Distance properties.
Sensing at a Distance
- Each artie has a means of sensing the attraction or repulsion of entities in
its environment. Action at-a-distance
is sensed in a 'straight' line metric for the given environment geometry. Each artie can have an arbitrary number of
sensing channels, each tuned to a different sensing metric. For example, an artie might have the ability
to sense red, green, and blue colour values of environmental objects using
different sensing channels. The effect
and quality of a given sensing channel can be an arbitrary function of the
straight-line distance from the artie to the sensed entity. For simplicity we can normalise all such
sensing actions to the scale of measurement of the sensing channel. All sensing can then be limited to the range
(0,1), with 0 representing no sensing or attraction, and 1 representing full
sensing.
Interpreting sensings as Attraction and
Repulsion - The result of sensing at-a-distance
for each artie is that each sensed entity receives an attractiveness score
based on the distance and quality of the observed entity, combined with a
'taste' function built into the artie that is sensitised to that observation
channel, entity, and distance by a transfer function. The artie uses this attraction and repulsion metric to guide its decisions
and behaviours. From the sensing
interpretation an artie can choose to re-act to these sensings. For example, an artie may choose to move
towards or away from a sensed item based on a transfer function of attraction
or repulsion. The transfer function can
also be used to change the artie or the environment based on a transfer
function. For instance, if an artie
senses something it is sufficiently repulsed by, it may emit a colour or gas
cloud akin to a skunk in self-defence. Likewise, it may decide to try and clone
or co-opt colours it highly likes in its neighbourhood. This makes an artie a type of rogue filter
that operates on a local neighbourhood, but is also able to help evaluate the
pertinence of its location or local neighbourhood against the sensing at-a-distance
metric.
2.1 Examples of
taste functions
Voting, Memory, and Collective Critique are three primary mechanisms of ‘taste’ in Arties.
A community of
arties, each with their own evolved (and evolving) attraction criteria can pass
collective judgement on the relevance of each point in an art space to the
preferences of the artie. This allows each artie to vote on how willing they
are to contribute to the changing of a given entity (or pixel) to satisfy their
curiosity. The sum of the votes cast by
a community or arties within a space is the collective pressure to change or
morph the art space to the preferences of the arties. Furthermore, each Artie
has the ability to remember its own collective history of past judgements in a
persistent local memory. This memory is
also how the knowledge space of a given Artie can be initialised, shared, and
compared with the memories of other Arties.
An Artie’s memory contains the attraction/repulsion reaction of the
Artie at a particular geometric co-ordinate at a given time.
3.0 Programming
Programming the
Artie - Arties are programmed by adjusting the distances of repulsion and
attraction and the strengths of repulsion and attraction at those distances. See drawing of attraction/repulsion
curve. If this curve is sufficiently
non-linear, it can be shown that the arties will exhibit attraction/repulsion
trajectories that fall into one of three guises – a fixed point, in which the
attraction and repulsion of the artie is in stasis, a limit cycle, in which the
trajectory of the artie stays within a fixed boundary (which may be chaotic),
and divergence, in which the path of the artie never approaches a fixed point
or stays within a predictable boundary.
The salient features of the attraction/repulsion potential curve become
weighted components in a genetic vector representation of the
attraction/repulsion within the artie.
These salient features are akin to inflection points and zero crossings
of a potential curve. Adjustment of
these parameters tunes the attraction and repulsion of the artie along various
sensing channels. Tied to this tuning
must be a cost or fitness function that helps the artie assess whether the
current configuration of its potential curve should be changed, and in what
direction. Note that this potential
curve can also be explained as the arties’ curiosity.
We anticipate that much Arties programming will be non-algorithmic or self-organising. Because of the non-linear nature of complex systems such as the Arties universe, it is difficult to program Arties by setting up their transfer functions and parameters to known values with a priori intent as to their behaviour and the artistic meaning of that behaviour. Programming Arties thus becomes an interplay between interactions that result in emergence from the interaction of Arties in the environment, reinforced by fitness function judgements and inputs by the meta-designer programming the Arties.
4.0 The Artie
Lifecycle
The operation of Arties in their environment is best understood by their lifecycle. Arties operate according to the following schedule of constraints and rules:
Constraint 1 –
Only 1 Artie can occupy a given (x,y) co-ordinate at any time t.
Constraint 2 – The
Arties’ universe is an NxN square of (x,y) co-ordinates.
Step 1 – Initialisation. Locate the Arties at an (x,y) co-ordinate
within the universe.
Step 2 – For each
sensing channel i, compute the resultant attraction/repulsion of the Artie to
each other (x,y) co-ordinate in its universe according to the following
relationships:
Xn,n = f1(Channeli(x,y)) * åxåyR(Distance(x,y))
/Distance(x,y) * x
Yn,n = f1(Channeli(x,y)) * åxåyR(Distance(x,y))
/Distance(x,y) * y
Where the Distance(x,y) function is ( ( n – x)2 + (n – y)2
) 1/2
Step 3 – Act upon the resultant vector according to the Arties’
design. At any step an Artie can
perform one or more of the following actions:
a.
Move from (Xt,Yt) to (Xt+1, Yt+1) [Subject to constraints of
co-occupancy]
b.
Vote or remember to itself its opinion at (Xt+1, Yt+1)
c.
Contribute to the collective vote for category j for its perception of
all points (x,y) at time t.
d.
Emit a new colour at (Xt+1,Yt+1), subject to a blending transform B(colour).
e.
Copy or carry a colour subject to a blending transform B(colour) for the pixel at (Xt+1, Yt+1)
f.
Evolve the attraction/repulsion transform R(Distance(X,Y)) using
genetic principles.
g.
Exchange attraction/repulsion DNA with another Artie, adjusted by an
inheritance transfer function I().
Step 4 – Deplete
the Arties’ energy balance according to the cost of performing the operations
in Step 3 (a-g). If the Arties’ energy
has annealed below a stability threshold, halt the system and remember the
system state as a quiescent snapshot of the system evolution. Otherwise, return to step 2 and keep the
system going.
Note that the
annealing relationship should reflect a form of exponential decay.
5.0 Results
Tests to date
have concentrated on understanding the sensing channel perception dynamics for
the Arties. Consider the following
initial Arties universe, which ironically enough is a picture of an Artie! This is a 128x128 24-bit per pixel bitmap
image.

Figure 5.1 Artie
The Arties view
this image as three sub-images corresponding to red, green, and blue channels
respectively as shown below.

Figure 5.2 Red Green Blue Channels
Lets look at
what an Artie ‘sees’ in these images along the red, green, and blue channels
when located at co-ordinate (0,0), looking toward (63,63).
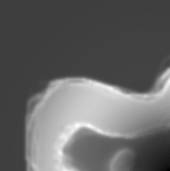
Here’s the red view
Figure 5.3 Red view
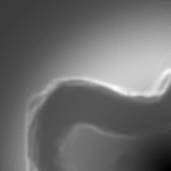
Here’s the green view
Figure 5.4 Green View
Here’s the blue
view
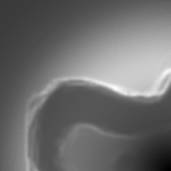
Figure 5.5 Blue View
5.1
Implementation Notes
The Arties
system just described is currently simulated using mathematical models using
the MathCAD 7 software from MathSoft Corporation. This simulation environment facilitates rapid prototyping during
the exploratory phases of designing the Arties’ universe. Of particular note is the ease of defining
new and complex transfer functions at the many places within the Arties’
dynamics that permit such transitions.
Appendix A contains the MathCAD 7 worksheet used to establish the basic
principles of Artie dynamics used in this paper.
5.2
Discussion
The Arties
universe is strongly motivated by advances in Artificial Life research. There is a growing literature relating the
fields of dynamical systems, chaos, cellular automata[5], self-organisation[6],
and theories of computability. For an
excellent overview of the interplay between these fields see Langton et. Al [7]. Arties diverges from this research primarily
in its intent. Much of the A-Life
literature is engaged in understanding the underlying forces and dynamics at
play in interacting systems of agents that exhibit biologically-motivated
interactions. At the present stage
Arties is more concerned with the generation of rich dynamics than in total characterisation
of how or why. The goal of Arties is to
provide a test-bed by which the learned attraction/repulsion of a system of
agents can be brought to bear on problems of meta-design. The ability of Arties to iterate over a
problem domain and to evolve their reactions to the tastes of the meta-designer
is key. Arties become true agents of
the designer.
Perhaps one of
the biggest deviations from classic A-Life research to date is Arties’ reliance
on human judgement as a necessary and integral component of the fitness
function. While a system of Arties does
exhibit strong self-organisational components, the solidification of such organisation
into persistent system characteristics will only happen if the ‘result’ of
applying the self-organised parameters is re-inforced by the fitness
function. Since an Arties’
reinforcement includes input from the designer building the meta-design
process, Arties acquire ‘tastes’ that reflect meaningful dynamics to those
perceiving their output.
6.0
Summary and Next Steps
Arties is one
approach to creating a system for supporting meta-design. Arties is part of an
on-going exploration of how to support meta-design in computer augmented design
systems.
We have
concentrated thus far on fields of attraction and repulsion as a primary source
of behavioural dynamics, but we can envision other such mechanisms including
families of probabilistic Cellular Automata, other survival landscapes, self-organising
and adaptive systems phenomena.
Some possibilities for on-going experimentation with Arties will be concerned with applying Arties-like systems in the areas of adaptive directives in Architecture, Object Structure Design, design of spatio-temporal behaviours (for games and simulations), virtual ambient spaces, and representation and computation of abstract design attributes.
References
[1] Gero J., Adaptive systems in Design: New Analogies from Genetics andDevelopmental
Biology, Adaptive Computing in
Design and Manufacture, Springer, 1998.
[2] Pontecorvo M., Designing the Undesigned: Emergence as a Tool for Design, Generative
Arts ’98 proceedings, Milan, 1998.
[3] Sims K., Evolving Virtual Creatures,
Siggraph ’94 proceedings, 1994.
[4] Holland J., Hidden Order: How Adaptivity Builds Complexity, Addison-Wesley, 1995.
[5] Toffoli, T., and N. Margolus. Cellular
Automata Machines. MIT Press,
Cambridge, 1987.
[6] Kohonen, T. Self-Organizing Maps. Springer-Verlag, Berlin, 1988.
[7] Langton, C. ed., Artifical Life II, Addison-Wesley, Reading, 1992.