Generating architectural spatial configurations. Two approaches using Voronoi tessellations and particle systems.

Paul Coates AA Dipl.

Christian Derix Msc Dipl Arch

University of East London School of Architecture & the Visual Arts

School\ of Architecture and the Visual Arts, University of East London, London, United Kingdom.

Email p.s.coates@uel.ac.uk

c.derix@uel.ac.uk

Ing. Stefan Paul Krakhofer MSc

School of Architecture and the Visual arts, University of East London, London, United Kingdom.

e-mail: krakarch@gmx.net

AbdulMajid Karanouh MSc

School of Architecture and the Visual arts, University of East London, London, United Kingdom.

Email: abdulmajeed_k@yahoo.co.uk

Abstract

It was one of the primary goals of the original Master’s programme in Computing and design at UEL in 1991 that we should work towards defining morphological generative processes for the conceptual design of architectural objects. These two papers offer a range of techniques which have been developed by two of this years MSc students (04-05) which show that we are getting close to this. The approaches range from computational geometric approaches (3d parametrics and voronoi diagrams) to emergent spatial orgaisation using agent based modelling. In many cases the resultant geometry is defined to the point where it can be transferred to advanced evaluation and fabrication systems, thus making this work sufficiently developed to begin to form a useful part in practical design processes.

Paper 1: Stefan Krackhofer Form evolution - organised spatial distribution

based on CA and Voronoi information

In my profession as an architect I aimed to develop a system, where space per se actively communicates its needs and reactions to changes in its environment. In contrast to many other professions and sciences; Architecture also has to create complexity and space. As such, collecting and processing of information becomes an important part of computable space in order to make and support decisions and consequently to change, adapt or manipulate space.

The implementation of a space-filling topological structure - the voronoi diagram - simulated the natural information exchange of particles in the environment. The voronoi approach subdivides the whole space into a set of sub-spaces according to the distribution of the objects. Each vertex represents a voronoi-cell and thus has its own Voronoi space which defines implicitly the spatial adjacency with the adjacent objects. Within the Voronoi cell, contained locations are closer to that object than to any other and thus creates a spatial relationship. The adjacent relationships between the spatial objects are reflected from the tessellation and are represented by the Delaunay triangulation.

The voronoi foam enables the collection of spatial information, the detecting of spatial characteristics which can be classified and organised into coherent pattern, as well as the manipulation of information and therefore space itself.

Supplied with the Voronoi information a new generated system starts to perceive and adapt and co-adapt itself to the environment according to its inherent nature (tasks or rules).

1.2. Introduction

Our environment as perceived is in a state of permanent flux, triggered by invisible forces of nature and the natural laws of feedback and relationship. Science describes, that naturally observed physical phenomena, from galaxies colliding with each other to quarks jiggling around inside a proton, can be explained by “fundamental interactions”, a mechanism by which particles interact with each other. Observing this mechanism closer we have to add, that particles do not directly interact with each other but rather generate a field, which affects the behavior of distant objects. Information or knowledge is transmitted through the medium of each particle’s individual field. The spatial environment can thus be understood as a complex system structured by relationships between particles. Consequently, we can note that the system’s manifestation as a spatial configuration communicates its inherent knowledge as visible information. Perceived space can thus be translated as a map of pattern of complex relationships between particles.

1.3. Personal Space

In my experiments I focused on the “field” and the data exchange within this medium. Exploring the field - the sphere of influence around particles, which I rather term the “personal-space” (PS), I derived a concept which is stated as follows: “Space is made up of particles and their relationships. Interaction and communication is made possible through their personal space and dependent on the neighbor relationship, based on CA principles.”

The developed analytical software tool generates a personal space around a vertex and detects its neighboring vertices for interaction. I translated this concept into reality by use of the computational geometries that are referred to as Voronoi diagrams and its dual concept Delaunay triangulation. However, in order to reach an authentic 3D description of space, the structures had to be translated into 3D. Thus, the Delaunay triangulation turned into a Delaunay tetrahedralisation and the Voronoi into a 3D Voronoi-cell.

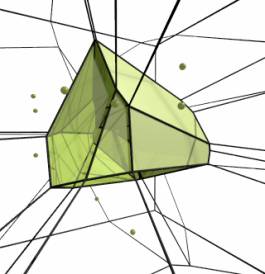
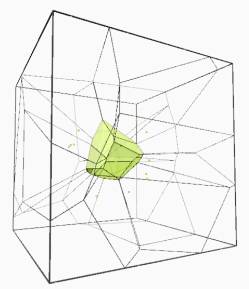
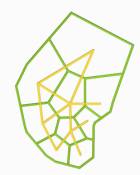
fig 1 3d voronoi

1.4. Description of the Voronoi approach

The Voronoi diagram generates a space-filling topological structure and is one of the most fundamental and useful constructs defined by irregular lattices, emphasizing its excellent applicability in modelling natural phenomena, the investigation of their mathematical, in particular, geometrical, combinatorial, and stochastic properties, and its computer-based constructability and representation. The Voronoi approach subdivides the whole space into a set of sub-spaces according to the distribution of the objects. Each vertex represents the center of a Voronoi-cell and thus has its own Voronoi space which defines implicitly the spatial adjacency with the adjacent objects (or the “influence space” of the objects). Within the Voronoi-cell, contained locations are closer to that object than to any other and thus create a spatial relationship.

1.5. Description of the Delaunay approach

The adjacent relationships between the spatial objects are reflected in the tessellation and are represented by the Delaunay triangulation, which maximizes the minimum angle of all the angles of the triangles in the triangulation. The triangulation of space defines the nearest neighbours of a vertex and generates a topological network.

1.6. Coupling of Voronoi and Delaunay

In coupling both approaches I generated a network of topological relationships such as connectivity, minimal-adjacency and maximal-adjacency. Further, the grouping and demarcation of equal or related entities can be conceived from the Voronoi-diagram.

The Voronoi foam enables the collection of spatial information, the localization of spatial characteristics which can be classified and organized into coherent pattern, as well as the manipulation of information and therefore space itself.

1.7. Application of the Voronoi foam

In the application, the procedure is described as followed:

During the initial - the preparation loop, all verity of the CAD–model are saved into “object” arrays and receiving the name of the object as their ID, which they are belonging to.

The observation loop generates the boundary condition for the system around the area which is defined to be observed. The user defines the boundary by drawing a box on the screen around the area of interest or the program chooses the edge of the CAD-model as its boundary.

Now the algorithm can start to compute the relationships by starting with the triangulation, followed by the generation of the Voronoi foam. Each vertex has its own Voronoi space and after checking the vertex ID, the vertices with the same ID are grouped together to evolve the object’s personal space. By now each vertex can receive information from their neighbors, since the system is based on CA principals. The information can be position, distance, volume, color, whether it is shadowed, temperature, ID, size of the whole object (bounding box), the amount of neighbors the neighbor cell has and so on.

1.7.1 Way finding

The Voronoi foam was than implemented as the background information into navigation, especially way finding. In order to find the shortest way from object “A” to object “B”, all boundary vertices of “A” ask their neighbours outside their personal space and they ask their neighbours and so on till they find “B”. This search approach evolves a network of interlinked tree-structures. The path between “A” and “B” can than be drawn by following the branches of the network. By now the path is “as the crow flies” and has to be corrected to the space in between the objects.

1.7.2. Occupation analyses

Another application for the Voronoi foam is in the occupation analyses of space. In that case the search agents are themselves the centre of Voronoi cells. During the search the agents receive information of the surrounded cells. If the information such as distance, brightness, height, …fits their inherent needs, the agent occupies this position.

fig 2 3d voronoi showing spatial organisation within a cube

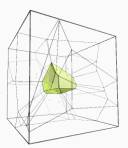
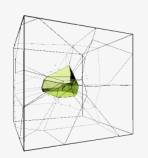
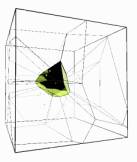
1.7.3. Space evolution

The active process of generating and evolving spatial forms demands the introduction of a process which leads to equilibrium among all entities of a system, the theory of self-organisation. In the context of architecture I find it more suitable to refer to this process as co-adaptation (structural-coupling) among the parts triggered by feedback.

“Form”, is the fixed goal in architecture and thus the aim was to develop an algorithm which generates “form” out of complex relationships among disorganised subsystems.

In order to apply a method of organisation, subsystems or functions have to be defined and set in dependency to each other and to general attractors. As such a clarification of the term “function” has to be found.

The Images below describe the process of space evolution. Starting with a self-organisation of functions followed by the application of the Voronoi foam.

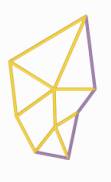
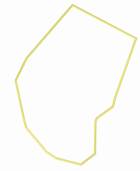
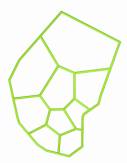
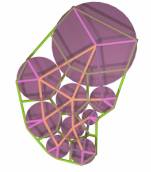
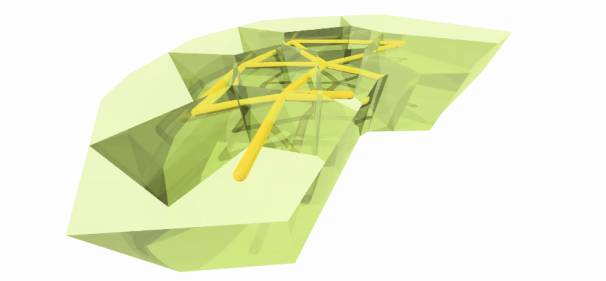
1.7.3.1. Feeling a pre - Image of Function

Function can generally described as the accumulation of needs, however, if we were to define function accurately, we have to consider that this demands knowledge of the occupants, their needs and desires, consequently their feelings. In order to take human feelings as the core motive for architecture we have to analyse human behaviour in their environment or interview them in order to translate the results into an algorithm which generates the pre-image of function.

This would be accompanied with a tremendous effort, yet, worthwhile since utilisation, size, proportion, orientation, and neighbour-relationships could then be derived.

As such, an efficient way of accumulating relevant data is to obtain the information from tradition, building-regulations or in case of competitions, from the “raum-program”.

Deriving the functions from the “raum-programm” was within the way I took. Starting with the translation of the “raum-program” into an array subdivided into sub-systems and organised according to their relationships. The sub-systems were then substituted by autonomous intelligent agents who have knowledge of their position in space, know who their nearest neighbour is, know who its aimed neighbour should be and its preferred orientation.

1.7.3.2. Self – organisation and boundary condition

By now the system is prepared and ready for the self-organising process to act on. Realising that we do not have the possibility of parallel computing, I decided to start the process, step by step, by increasing the fitness of one agent after another, until the topological network is reached. Followed by activating external attractors, such as feedback of the occupied space, sun, orientation and shadowing, which led to unexpected chaotic phenomenon and finally to the collapse of the system. It turned out, that the direct interconnection of subsystems did not allow any adaptation, since this would simultaneously result in the loss of fitness. In other words, the demarcation or boundary conditions had to be rethought.

The nature of the boundary between entities became a serious question. I observed that the highly fluctuating dynamics of interacting subsystems were triggered by small changes of their position, even when one subsystem was in equilibrium. This phenomenon caused an imbalance of the whole system and resulted in a permanent fluctuation, never (at least not for a very, very long time) reaching equilibrium.

Struggling with this problem I remembered how I started to design with paper and pencil (outside under the sun, relaxed, free and independent), even with wobbly strokes it was relatively easy to develop design. Or, do I now realize that the wobbly stroke was exactly the cause for a good development? Musing on this fact, I realised that the system demands a wobbly stroke. I came up with the concept of a precise system encased within a viscous medium that allows for uncertainties. If the optimal orientations of two functions in a precise system are incongruous to one another, the positions of the other functions are compromised as they are directly moved out of place by the local optimisation. Whereas, in a viscous medium, the functions are able to move freely around the centre of their axes without disturbing the adjacent functions, allowing for an overall optimisation. Consequently, we have to pay special attention to the medium as it assumes an active task and therefore requires a dimension; in other words, an embodiment.

First I rejected the idea that a system inside a system requires a system to exist, but I realised that this is exactly the case. The boundary maintains the equilibrium of its inherent systems even when the boundary’s environment is fluctuating because it can absorb a certain amount of turbulences and stress.

Developing this idea of absorbing and balancing further in an architectural-engineering context, structural tasks can be assigned to the boundary-dimension. Considering that all systems are nested and exchanging information, force visualised as information can be trickled through the system so as not to irritate it but arrives at its destination where it can be absorbed.

In all, my concept illustrates the implementation of functional organisation with structural trajectories, which are enclosed within the boundaries. It is obvious that another dimension of feedback evolves within this constellation, which I would define as mutual (co)adaptation. Before the subsystems reached equilibrium they already altered the “form” of the whole system. The system feeds back the “new” information about “external”-forces which needs to be carefully diverted through the system. Continuing this process results in “general” equilibrium, or as I would call it in the vocabulary of architecture: aesthetics, where beauty originates from needs.

1.8. Conclusion

Generating spatial effects enabled through simulating phenomena of space, material, light, wind, sun, sound, or behaviour clarifies that architecture is increasingly becoming a simulation rather than a representation of space.

The study of architecture therefore has to consider simulation as a powerful design-tool, in order to understand and implement complex relationships. The educational nature of simulation shows itself when developed through the use of algorithms in programming, altering the study of architecture. In carrying out experiments and writing algorithms, I learnt that the ability to identify pattern is fundamental to the design process. As such, the personal interaction between student and algorithm supports an increase in the understanding and knowledge about patterns, their relationships and compatibility. This process trains one to work with pattern since experience can be gained from feedback, whether visually or accoustically, triggered by the students’ decisions and actions.

The “system-view” of architecture which has the goal of designing a system rather than a form will change the way we study and practice architecture; and will likely lead to an increase of quality in architectural design.

In order to facilitate this shift, designers should strive for a conscious transfer of authorship. Following my experiments, my position evolve from the role of dictating the behaviour of subsystems to the role of coordinating them which can be illustrated by the following analogy: from an audience’s point of view, the conductor dictates how the orchestra should play the music and is the driving force behind the musical performance. From the musician’s point of view however, the role of the conductor is not to dictate but to improve the whole by coordinating creatively. He is merely piecing the entities together into a harmonious whole. He is no longer the centre of the performance / design but part of it.

As such, the definition of architecture is becoming more complex than before, but with the significant advancement that the architect is not the centre of change, but an important conductor in the system. The system “architecture” interpreted as a subsystem of our environment led to the research in nature. In all, nature is an open system with inherent invisible laws of feedback and relationships which strive for equilibrium. The tendency towards equilibrium is manifested in the process of self-organisation. The result of this unique process is form. Ultimately, nature knows best how to create form, not in the sense of a random shape as we commonly perceive form to be, but as an equilibrium between entities. If we are to be as good of a designer as nature is, we must find a way to successfully implement the process of self-organisation into architectural practice. The results of my experiments of self-organisation showed a promising first step in its applicability in architecture. Although the algorithms did not perfectly organise the entities, the final form was a satisfactory compromise.

We must realise that natural design is merely “good enough” to fulfil specific tasks in relation to its environmental system. It is barely optimised for these specific tasks, forever a good compromise between all entities in a whole.

I was able to exploit a sliver of the playground of biological evolutionary systems, yet there is so much still to be uncovered in Mendel’s garden of architecture.

Paper 2: AbdulMajid Karanouh Architecture, Agents, & Hyper-Surfaces:

High-Tech Building Envelope Generative Design

2.1 introduction

We have always admired and observed how natural systems are generated in nature and how different intelligent technologies and behaviours emerge during the generative process and how superior those technologies are to the ones we use to generate and construct our own designs and systems. We understand that all elements of any system found in nature, whether ‘live’ or ‘dead’ ones, take part in the formation and generation of the system’s complexity by the numerous interactions that take place among those different elements themselves and among other elements of neighbouring systems as well, thus establishing an infinite network of data exchange in its various existing forms, states, and magnitudes, connecting together not only all systems found in nature, but also all systems found in the universe. This might interpret the superior intelligence of natural systems in nature and the universe and the great harmony in which they coexist.

From nature we discover that all systems behave like swarms where groups of agents of various types and behaviours following simple rules can generate the simplest to the most complex forms and designs. For this purpose, we have to be able to design systems made up of virtual agents that can behave like swarms, self design, and self organize themselves and their positions and relationship in 3D space.

Computation may not be the best solution ever for this task, but its flexibility, data storage capacity, speed, and accuracy makes it a convenient choice for now.

Many complexities arise from generating nature-like form buildings of which one of the most critical and delicate case is the building envelope. Computation can help us explore ways to generate complex surfaces with integrated mapping, pattern, and structural elements and pave the way for Mass Customization.

Two different conceptual approaches can be used to develop generative design process;

Emergent Generative Design: Agents will be given simple rules to follow with little movement restriction. The swarming behaviour of the agents will be left to self organize their position in 3D space from which some unplanned forms and structures may be expected to emerge.

Parametric Generative Design: Agents will be given more defined rules to follow based on mathematical relationships associated to controllable parameters where if one parameter of a group of agents is changed, the parameters of other groups will self adjust and the agents will self organize to accommodate the new modification.

Agents under Emergent or Parametric computation rules can represent anything from the users to the very finite building components and nodes interacting together and responding to abstract positive and negative mathematical force fields with controlled magnitudes.

With this bottom up approach complex systems and forms can be generated from simple, finite, less complex, and self organizing agents.

2. 2 Preamble

Designers in the architectural domain have mostly been interested in studying natural complex emergent designs and forms that involve inhabitants living in communities like the anthills, beehives, bird nests, and other similar systems and geometries which we generally refer to as Organic Forms and lately as Blobs. Free-form designs, generally known in the architectural field as Organic Architecture and lately as Blobs. The dominant formal vocabulary of blobs is their generally double-curved surfaces which have special functional, spatial, structural, and aesthetic characteristics compared to common buildings as we know them today.

Architects face several problems when dealing with blob designs, mainly as follows:

A- Design Concept

There is no established principle or theory concerning the design and production of natural complex forms that can be a useful source providing feedback to the designer especially in the conceptual design phase.

B- Structure & Pattern Integration

In a common CAAD environment, complex geometric forms generally exist as surfaces without structural, material, mapping, or functional considerations. Although several advanced CAAD packages are available now, still, the engineering and technical aspects cannot yet be tested in common design visualization software [Klinger 2001].

fig 3 some parametrically defined morphologies

C-Data Exchange & Fabrication

3D data exchange between CAAD/CAM/CAE applications has not yet become a standard process, thus the fabrication and production of the mass custom components is still considered as a major barrier by most practices due to this missing link of data flow and relative high cost, and thus avoid exploring further methods for generating blobs.

Design Automation using both Emergent & Parametric Generative Design can integrate the vast data related to A, B, & C by utilising agent based computation rules where different components are generated from different groups of agents. Each component is generally unique in size and position in 3D space. The data generated from the Design Automation process will be digitally used for Automation Fabrication and thus paving the way for Mass Customization [ONL 2003].

2. Conceptual Approach

Swarm Intelligence: Simple rules will be used and constantly modified to explore the various behavioural changes within one swarm, and the general behavioural changes among different swarms and those changes will result in various generated forms.

Bottom Up Design: By starting the design stage with the finest and simplest agents and elements that will gradually generate the whole complex system.

Biomimetics Extrapolation: A mix of biomimetic extrapolations will be demonstrated in one of the experiments to generate a form and its structure with CAD by using both implicit modelling and explicit programming oriented modelling.

2. Computation Principles

Agent: Based on the principles of Nanotechnology, Swarm Intelligence, and the Bottom Up approach for generating complex systems starting by less complex actuators, Agents will be used in groups of various types to represent various elements of the building envelope and various elements of the context.

Hill Climbing: as the Agents will be able to learn and adjust by changing their attraction or repulsion reaction towards other agents according to how they perceive the changes taking place around them and thus set their 3D space.

Self Organization Map, as the Agents of the Swarm will be self organized based on simple rules follow. The will be able to check their neighbouring Agents of the same Swarm, and the Agents of Neighbouring Swarms and self organize themselves according to their position in 3D space and the behavioural rules set for them.

Mapping, Agents will connect each other with elements according to different rules, thus generating different meshes, tessellations, patterns, and structural guidelines integrated into the generated envelope.

Fig 4 Netlogo project interface

2.3. Experiments

The experiments will be divided into two categories based on two different conceptual approaches and carried out with different software and programming languages; Emergent Generative Design using NetLogo 3D-Logo, and Parametric Generative Design using AutoCAD-Visual Basic for Applications (VBA).

2.3.1 Emergent Generative Design

The general idea of this approach is that no pre-determined forms are set in the computation code. Simple abstract rules are given for the agents to follow and unplanned collective behaviours might be expected to build up from groups of various types of agents and thus unexpected forms might emerge during the process.

The Turtle is the name used in NetLogo 3D to describe an agent. There will be 4 types of turtles used in the following experiments:

Common Turtles [CT] agents representing the surface nodes swarm as grey spheres

Unique Turtles [UT] agents representing the swarm that can only dominate the nodes swarm as yellow spheres

Supreme Unique Turtles [SUT] agents representing the swarm that can dominate the nodes and unique swarms as red spheres

Edge Turtles [ET] the agents representing the connections and mapping generated by the nodes as blue cylinders.

The force field around each agent is represented with another sphere of the same but slightly intensity reduced colour.

The Algorithm:

1. Each Agent scans every other agent and measures its relationship and distance to it.

2. Check own force field and other agent force field and compare to the separating distance.

3. If separating distance is greater than force field then travel forward 1 step module, Else repel backwards 1 step module.

4. Grey CT agent checks for closest neighbouring CT agent and connects it with an ET agent.

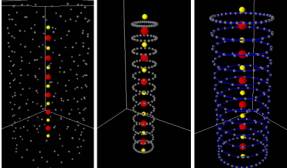
Fig 5 CTs forming spirals ETs forming basket-structure

Trusses emerged at each floor level

Trusses emerged at each floor level

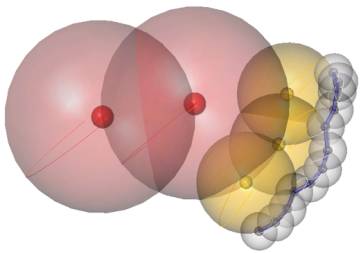
Fig 6

The image above shows the attraction and repulsion relationship between different agents. Notice that the Red SUT Agents are positioned at each others´ force fields bounding spheres and not being influenced by other agent types. The Yellow UT Agents are positioned at both their own and Red SUT Agent’s force field spheres and not being influenced by the Grey CT Agents. The Grey CT Agents are bounded by their own and Yellow UT Agents’ force fields and being influenced by the Red SUT force field. The Blue ET Agents are the cylindrical members connecting the CT Agents. The images in Fig 5 (representing a building with its core) and bottom Fig 6(representing blob of blobs) show clearly how different forms, patterns, and structures can emerge from the simple rules and relationships given to the agents to follow.

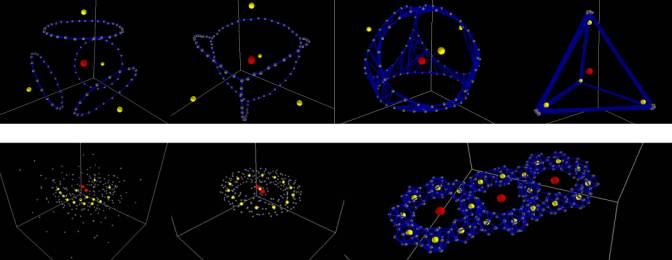
Fig 7 more emergent morphologies using Net Logo

fig 8 steps 1 – 6 referred to in the text below

2.3.2 Parametric Generative Design

The concept of generating complex forms and mappings from simple rules will be maintained as a major part of the whole approach criteria in this section as well, but there will be no forms or mappings emerging unexpectedly. Everything will be carefully planned and agents will operate according to well set mathematical equations, and parameters. The exact position of each agent will not necessarily be predicted rather than the general form, mapping, and structure expected to be generated. The agents will still self organize and self learn, but restricted to follow a well defined order.

The Algorithm:

1- the ‘seed’ is set and the node-agents (yellow dots) take the form of a cylinder and are ready to interact

2- the source-agents are then inserted (4 red spheres in this case)

3- each node-agent will scan its surrounding checking its distance with the neighbouring node-agents simultaneously and the its distance to the source-agents consecutively

4- The node-agents will check each others’ results, and will arrange themselves in order, starting from the closest node-agent to the source-agent (winning node) down to the furthest one.

5- The closest node-agent will travel the longest step towards the force-agent. The step is proportional to the distance between the winning node-agent and the source-agent. The rest of the node-agents will follow in with shorter steps according to a distance proportion parametric equation.

6- Upon each time frame or replication, the node-agents will again check the distances and rearrange themselves and reduce the magnitude of their next steps to accommodate the new conditions accordingly. This process as explained previously is called Self Organization Map and Hill Climbing self learning.

7- At the end of the final time-frame, the node-agents have already taken their final positions in 3D space. A skin is generated to wrap the point cloud determined by the node-agents.

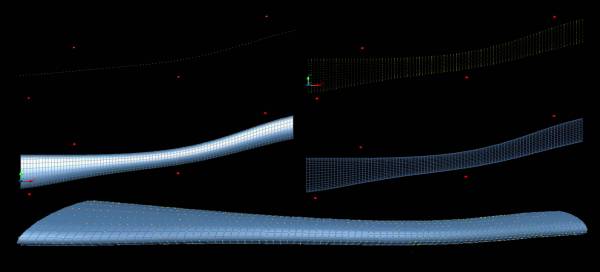
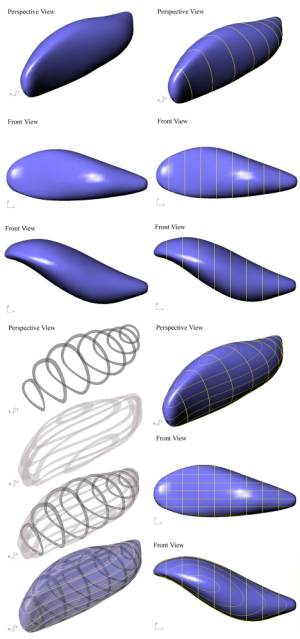
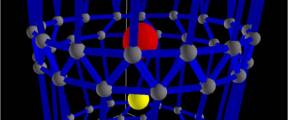
Fig 9 parametrically deformed tubes (force nodes in red)

Image on the leftfig 10 shows the development of a complex blob from initially a spheroid. . This node-agents of the spheroid interact with the source fields (red spheres) and begin following parametric equations and rules and adjust their positions accordingly.

Below,Fig 11 initially modelled in Rhino, the concept was to develop a blob inspired from both the drop of water and radial structures like the sea urchin and spider web. The red source points represent the self weight of the water drop and the blue source points represent the drag force generated by the wind when freefalling. The positions taken by the node-agents at the end of the process are wrapped with a mesh.

Figure 10 complex blob from spheroid

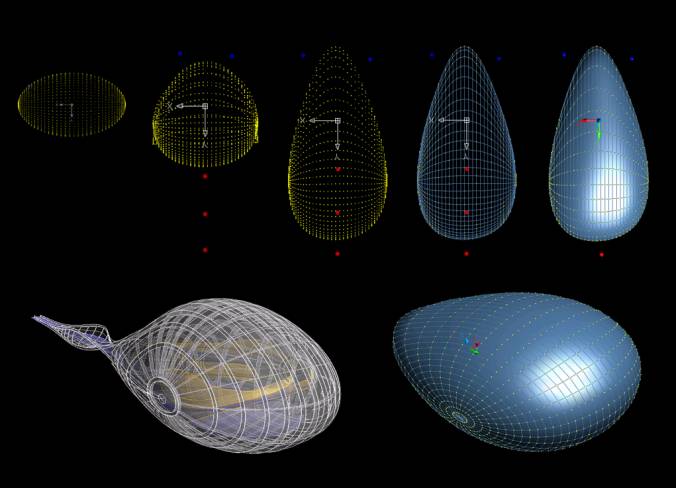
figure 11 see notes above

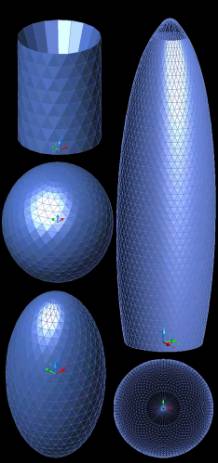Fig 12

The images left show clearly the mathematical sequence followed to reach to a form similar to Fosters’ Swiss RE

The below fig 13 on the right show clearly the mathematical sequence followed to reach to a form similar to Fosters’ Swiss RE

Below Fig13 is a series of tests carried out to see how different meshes with different patterns can take shapes and forms generated from well defined mathematical equations. Dividing the agents into different groups within one mesh allows the user to insert more than one equation into one mesh, thus creating a more complex shape and also providing more control.

Fig
13

References:

Section 1

[1] Ludwig von Bertalanffy, “General System Theory - Foundations, Development, Applications”, George Braziller, New York, 1968

[2] Wolfram Stephen, ”Statistical Mechanics of Cellular Automata”, Reviews of Modern Physics, 55: 601-644, 1994

[3] Wolfram Stephen, ”Computation Theory of Cellular Automata.” Communications in Mathematical Physics, 96: 15-57, 1994

[4] Wolfram Stephen, “Theory and Applications of Cellular Automata”, Singapore: World Scientific, 1994

[5] Weiss P.A., “The basic concept of hierarchic systems”, Hierarchically Organized Systems in Theory and Practice, New York: Hafner, 1971.

[6] Resnick Mitchel, “Turtles, Termites and Traffic Jams: Explorations in Massively Parallel Microworlds”, Complex Adaptive Systems. Cambridge, Massachusetts: MIT Press, 1997

[7] Bonabeau E., Dorigo M., Theraulaz G., “Swarm Intelligence: From Natural to Artificial Systems”, London, Oxford University Press, 1999

[8] Camazine S., Deneubourg J.-L., Franks N. R., Sneyd J., Theraulaz G., Bonabeau E., “Self-Organisation in biological systems“, Princeton, Princeton University Press, 2001

[9] Salthe S.N., “Self-organization of / in hierarchically structured systems”, Systems Research 6: 199-208, 1989.

[10] Salthe S.N., “Development and Evolution: Complexity and Change in Biology”, Cambridge, MA: MIT Press. 1993, a.

[11] Ashby W. Ross “Principles of the Self-Organizing System“ In (Von Foerester and Zopf Jr 1962), pp. 255 - 278.

[12] Holland John H., “Emergence: From Chaos to Order”, Reading, Massachusetts: Addison-Wesley, 1998

[13] Holland John H., “Adaptation in Natural and Artiffcial Systems: An Introductory Analysis with Applications to Biology, Control, and Artiffcial Intelligence”, Cambridge, Massachusetts: MIT Press, 1992

section 2

Bob Berkebile and Jason McLennan, The Living Building-2004

Dennis Dollens, Toward Biomimetic Architecture, University of Florida • January 2005

ONL, Swarm Architecture-2003

ONL,, Acoustic Barrier-2001

ONL, Hyperbodies-2004

Jesper Hoffmeyer, The Swarming Body-1994

Yahya, Designing Nature-2004

Yahya, The Miracle in the Ant-2004

National Nanotechnology Initiative-2005

David Gordon Collective Intelligence in Social Insects-2005