The Generative Dynamics of
X, Y & Z Coordination
Manuel A. Báez,
Architect, B. Arch., M. Arch.
Co-ordinator: Form Studies
Unit, Foundation Year and Admissions
School of Architecture,
Carleton University, Ottawa, Ontario, Canada
e-mail: mbaez@ccs.carleton.ca
Abstract
The architectural work-in-progress
titled the Phenomenological Garden
has been exploring the morphological and integrative potential of cellular
units generated by fundamental processes within natural phenomena. As part of the overall objectives of this
project and the Forms Studies Unit at Carleton University’s School of
Architecture, students in the Crossings
Workshop have been carrying out these explorations through projects that
incorporate hands-on procedures derived from the research. The inherent properties of the cellular
units, along with the nature of the materials and processes involved in these
projects, allow for a generative and intuitive learning process to occur. Previously, the generative dynamics of
two-dimensional cellular units have been explored (see the Paper: Generative Dynamics: Process, Form and
Structure, 2004 Generative Arts Conference Proceedings). This paper will
present the work that has emerged from the exploration of the X, Y and Z
coordinate system as a fundamentally dynamic relationship within a generative
cellular process.
1.
Introduction
“In this brief account of coordinate
transformations and of their morphological utility [The Theory of Transformations, or The
Comparison of Related Forms] I have dealt
with plane coordinates only, and have made no mention of the less elementary
subject of coordinates in three-dimensional space . . . And that it would be
advantageous to do so goes without saying, for it is the shape of the solid
object, not that of the mere drawing of the object, that we want to understand;
. . . But this extended theme I have not attempted to pursue, and it must be
left to other times, and to other hands.”
D’Arcy
Wentworth Thompson [1], also see Fig. 1
Throughout the natural environment
we find fundamental processes that generate versatile systems and patterns. These highly fertile, self-organizing and
regulatory processes inherently exist within, and generate, the rich realm of
natural phenomena. Simultaneously, they
are composed of, and self-generated by, elemental geometric relationships that
gradually evolve into versatile integrative systems with startling form and
structure generating capabilities.
Through the systematic analysis of the versatility and generative
potential of these systems and their interrelated cellular patterns, new
insights can be revealed into the emergence of complex morphological structure
and form. The intrinsic nature of these
dynamic patterns reveals that they are cellular configurations of highly ordered
relationships. The extremely dynamic undulations
of the flow of energy are constrained within the apparently static stability of
the pattern. This versatile
constrained activity fluently encodes the emergent pattern with complex potentiality
offering a multitude of possible or alternative ‘readings.’ The cellular units comprising these
patterned networks innately contain
the intrinsic attributes of the versatile processes that generate them. Inextricably, we are participants in, and
surrounded by, this rich and dynamic matrix of natural phenomena. The inherent properties and characteristics
of this generative matrix can be systematically explored allowing for the
possibility of insightful understanding of its fluent potentiality. This analytical process offers new insights
into the nature of the reciprocal
relationship between matter, developmental processes, growth and form. Rich educational methodologies are offered
through new procedures and techniques that can inherently allow for intuitive
learning through self-discovery. The Phenomenological Garden project is a
work-in-progress and in-process that has been inspired by these insights and
the working procedures that they can reveal regarding nature’s developmental
processes. It seeks to explore the form
and structure generating potential of these dynamic processes along with their
elemental components, emergent integrative properties and pattern generating
capabilities.
2. Elemental Cellular
Dynamics
Through systematic analysis, the
dynamic potential of basic geometric relationships has been explored, leading
to the development of a series of flexible cellular units and hands-on
analytical
procedures. Inherently, this allows for intuitive
discovery to occur regarding the interrelationships between form, structure,
and generative process. The cellular
units are constructed using bamboo dowels and joining them together with rubber
bands thus creating a very malleable joint.
By combining these very flexible units together into three-dimensional
configurations, the form generating potential of both the individual cells and
the cellular assemblies can be easily explored. The flexibility of the joints and their complex three-dimensional
relationships, generate a wealth of forms and structures through the emergent,
transformative and organizing properties of the integrated assembly. The dynamic properties of initially
two-dimensional cellular units have been explored (see the paper: Generative Dynamics: Process, Form and
Structure, 2004 Generative Arts Conference Proceedings). These have been hands-on dynamic
explorations of what were primarily graphic, two-dimensional and static explorations
by D’Arcy Thompson [1] through his “Theory
of transformations or the Comparison of Related Forms” (see Fig. 1 below).
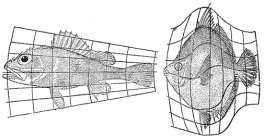
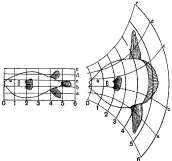
Figure 1: D’Arcy Thompson, grid or coordinate transformations of graphic
depictions of biological forms [1].
As he recommends in the
introductory quote above, Thompson’s “extended theme” of three-dimensional
coordinate transformations have been explored through investigations of the
generative dynamics of such complex assemblies. The following is a presentation of some of the forms and
structures generated from the emergent properties of several intrinsic
combinations of a cellular unit that is a dynamic three-dimensional assembly of
the X, Y and Z system of co-ordination.
2. X, Y and Z Co-ordination
In Figure 2 we see
four views of a cellular unit constructed with 12" and 5" bamboo
dowels and joined together with rubber bands.
The unit is composed of three surfaces (or planes) at right angles to
each other with each surface being defined by four 12" dowels assembled
into a grid of two pairs at right angle to each other and four 5" dowels,
one at each end of the 12" pairs (see Figure 2 D). The three surfaces have a high degree of
transformability due to the flexibility of the joints and each surface defines
one of the X, Y and Z coordinate directions in three-dimensional space. Each surface can fully collapse along the
two orthogonal diagonals of the assembled grid. They can also be warped into a transformable, collapsible and
highly flexible hyperbolic paraboloid.
Three-dimensionally, this cubic cellular unit (or module) is composed of
several interacting degrees of freedom through the combination of flexible
joints (a total of 42). From another
perspective, this complex intermingling is also the interactions of the three
flexible hyperbolic paraboloids within the three-dimensional assembly. In Figures 3 and 4 we see several
configurations that can be generated from this dynamic interplay.




A B C D
Figure 2: Views of the X, Y & Z Cellular Unit: 12"
and 5" bamboo dowels and rubber bands.
Three planes at right angles to each other: D clearly shows one of the planes with the central diagonal edges
of the other two; B & C show views through the four diagonals
of the cubic assembly.
In Figures
4 and 5 we see
several of the transformations that can be generated from the cellular unit
through a systematic hands-on investigation of its dynamic properties. In the Crossings
Workshop, students have been exploring this cellular unit along with the forms,
structures and dynamic properties that emerge when several of these units are
combined. The numerous possible combinations
lead to unexpected overall patterns and dynamic arrangements that generate new
and diverse developmental directions for the assembling process.

A B C
D
Figure 3: The Cellular Unit and several of its basic
transformations. A: The Cellular
Unit. B: Flattened assembly along one of the four diagonals of the cubic
assembly. C: Collapsed assembly
centered around one of the four diagonals.
D: Collapsed X, Y and Z axes
with 5" dowels removed (see Fig. 5).




A B C D
Figure 4: Different transformations of the Cellular
Unit. In A the 5" dowels have been removed. Each one of these configurations becomes the “modified” cellular
unit that is then assembled together.
A B B






C D E
Figure 5:
Different stages of a cellular unit that can completely collapse into the X, Y
and Z axes (A & B) and gradually expand into a
tetrahedron (C, D, E and F).
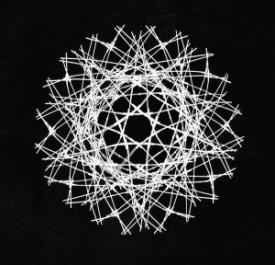

Figure 6: Two views of the same
construction, by M. Báez, using the cellular unit shown in Fig. 3. The construction is a dodecahedron that
emerged from the assembling process.
Throughout the structure and the generated patterns one can discern the
squares, pentagons, triangles, hexagons, cubes and tetrahedrons that are
intrinsically embedded within the dodecahedron.


Figure 7: Cellular Constructions. Left:
By M. Báez, constructed with the same unit as in Figure 6 and exhibits the
same properties. Right: By Sarah Amirault, constructed using the
unit shown in Fig. 4 B. Different
patterns are revealed throughout these constructions. The X, Y and Z axes can be clearly seen in the overall pattern of
the construction on the right.
In Figures
6, 7, 8, 9 and 10 we see
several forms and structures that can emerge as the assembling process
gradually evolves into more complex configurations. Figures 6 shows two axial views of the same construction. This particular assembling process generated
a dodecahedron that was not preconceived nor initially anticipated. Cellular units (as shown in Figure 3 A) were
assembled together using their inherent properties as the guiding
principles. Within the resulting
three-dimensionally dynamic pattern of the form one can discern the complex
interweaving of the rich geometric properties of the dodecahedron: cubes,
tetrahedrons, hexagons, pentagons and golden rectangles (to name a few) in a
reciprocally complex relationship.
Several of these shapes can be discerned in the two views provided. Figure 7 is another construction generated
through the same process as in Figure 6 and also reveals the same level of
complex multilayering of forms. On the
right side we see a construction that incorporates the cellular unit shown in 4B
and the X, Y and Z axes of the initial cellular unit are equally prevalent at
this level of evolving complexity. The different modifications to the original
unit in Figure 2 lead to the emergence of totally different complex patterns
and dynamic properties.

Figure 8: Cellular Constructions, Study models by M. Baez, constructed with the
unit in Fig. 3. On the left are two
views of the same model and on the right are three views of another.
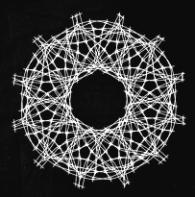

Figure 9: Cellular Constructions. Work by Ana Lukas constructed with the unit
shown in Figure1. Top view on the left
and under construction on the right.


Figure 10: Cellular Constructions. Work by
Michael Putman, Patrick Bisson and Rheal Labelle, constructed with the unit in
Figure 3. Top view on the right and a
side view on the left.
Figure 8 shows study models
constructed with the cell shown in 3A.
On both the right and left sides we see different views of the same
construction. Figures 9 and 10 show
views of two other constructions that have been developed to a more complex
level than the ones previously shown.
The transformability of the cellular units generates very different
overall complexity throughout the larger assemblies. Figure 9 shows a toroidal construction that was assembled with
the same unit and procedures used in Figures 6 and 7 (left side). The form shown on the left side of Figure 6
fits directly into the central opening of the form shown in Figure 9 (left
side). By comparing the two views shown
in Figure 9, one can see the dynamic diversity within the elaborate pattern. Figure 10 shows the most complex
construction that has been made with the cellular unit used in Figure 6. On the right side we see the top view
through the main vertical axis of the elaborate assembly and on the left, a partial
side view. The elaborate pattern is
ever changing throughout the structure.
Overall, the emergent patterns are at times reminiscent of the patterns
generated by vibrations in liquids and in thin layers of fine powder. Throughout all of these constructions,
dynamic patterns emerge with an ever-evolving intricate level of
complexity. Paradoxically, within the
integrative interactions of this complexity lurks the simplicity of the
original cellular units.
2. Conclusion
“We have been trained to think of patterns, with the exemption of those
in music, as fixed affairs. It is easier and lazier that way but, of course, all nonsense. In truth, the right way to begin to think
about the pattern which connects is to think of it as primarily (whatever that
means) a dance of interacting parts and only pegged down by various sorts of
physical limits and by those limits which organisms characteristically impose.”
Gregory Bateson [2]
The rich diversity found throughout nature’s processes challenges
our creative imagination and common sense because of its reciprocally related
combination of dynamic complexity and simple organizing principles. The work-in-progress presented here, along
with the broader goals of the Phenomenological Garden, inherently
address this fundamental paradox through multidisciplinary research and an
integrative working process. Such an
approach offers new possibilities and directions to the fields of morphology,
architecture and other creative disciplines at a time when there is an
increasing interest in the broad implications of our deeper understanding of
Bateson’s “dance of interacting parts” throughout the physical world.
References
[1] D’Arcy Wentworth Thompson, On
Growth and Form. Complete Revised
Edition: Dover, p. 1087. 1992. Chapter XVII covers The Theory of
Transformations, or The Comparison of Related Forms (P.1026-1095).
[2] Gregory
Bateson, Mind and Nature, Bantam
Books, p. 13-14. 1980


























