What is Generative Art?
Complexity Theory as a Context for Art Theory
Philip Galanter, BA, MFA
Interactive Telecommunications Program, New
York University, New York, USA.
e-mail: galanter@nyu.edu.
Abstract
In this paper an attempt is made to offer a definition of generative art that is inclusive and provides fertile ground for both technical and art theoretical development. First the use of systems is identified as a key element in generative art. Various ideas from complexity theory are then introduced. It is noted that systems exist on a continuum from the highly ordered to the highly disordered. Citing examples from information theory and complexity science, it is noted that highly ordered and highly disordered systems are typically viewed as simple, and complex systems exhibit both order and disorder. This leads to the adoption of effective complexity, order, and disorder as organizing principles in the comparison of various generative art systems. This inclusive view leads to the somewhat surprising observation that generative art is as old as art itself. A number of specific artists and studies are discussed within this systems and complexity theory influenced paradigm. Finally a number of art theoretical questions are introduced to exercise the suggested generative art definition and implicit paradigm.
1.
Introduction
I teach a course titled "Foundations of
Generative Art Systems" [1] and the most frequent question I am asked is
"what is generative art?"
Generative art often seems like a fuzzy notion, and most students don't
seem to "get it" until very late in the semester. And indeed, in forums such as the eu-gene
mailing list (http://www.generative.net) this very question has sparked considerable
controversy. In opening this paper I
would like to gratefully acknowledge the many discussions on this topic I've
had with both my students and the eu-gene online community.
Some might wonder whether the attempt to define
generative art is an empty pedantic exercise.
I hope that this paper will show that it is not. First clarity of language enhances any
discussion, including those about art and specifically generative art. Additionally the discussion of what generative
art is stimulates the discussion of other art critical concerns.
2. Two Views of the Term “Generative Art”
First a quick look at the term “generative art” from
the bottom up, and from the top down.
2.1 From the Bottom Up – Clusters of Current Generative Art Activity
With regard to the "what is generative art?"
question one is often reminded of the parable of the blind men and the
elephant. One blind man feeling the leg
of the elephant says, "Surely an elephant is like a mighty
tree". Another blind man, holding
the trunk of the elephant says, "Surely an elephant is like a large
snake". Yet another blind man,
placing his hands on the sides of the elephant, exclaims, "Surely an
elephant is like a great whale".
And so on. In a similar way
artists seems to all too often define generative art as being most like the
work that is closest at hand, namely their own generative art.
And indeed there are clusters of contemporary
generative art activity that are, in many ways, worlds onto themselves. Some of these include:
Electronic Music and Algorithmic Composition - Dating at least to the seminal paper by Brooks,
Hopkins, Neumann, and Wright in 1957 [2], those in the electronic music
community have explored all manner of generative processes for the creation (at
the macro level) of musical scores and (at the micro level) the subtle
modulation of performance and timbre.
This activity has not been limited to academic music. A recent article
in Electronic Musician, a magazine for working musicians, notes more than a
dozen programs using techniques as varied as cellular automata, fractals,
a-life, L-systems, chaos, and of course randomization. [3]
Computer Graphics and Animation
- Well documented in the
vast body of literature published by the ACM SigGraph organization and others,
computer graphics researchers have contributed to the realm of generative art
for decades now. Examples of generative
breakthroughs would include Perlin Noise [4] for the synthesis of smoke, fire,
and hair imagery, the use of L-systems to grow enough virtual plant life to
populate entire forests and valleys [5], and the use of physical modeling to
create animations that depict real world behavior without requiring the
animator to painstakingly choreograph every detail. These efforts have yielded results that reach far beyond the
research community. Examples include
animated feature length films such as those by Pixar and the hugely popular
realm of video game machines.
The Demo Scene and VJ Culture -
Borrowing from the
above, youth culture movements are taking generative technology out of the well
funded labs, recording studios, and animation companies, and adapting low cost
alternatives for use in nightclubs and other social settings. For such artists and enthusiasts generative
art is no longer obscure or esoteric, but rather an everyday method of creation. Randomization is the most frequently
discussed technique, but others are working their way into the scene as well.
Industrial Design and Architecture
- Design practice has
always included the iterative process of creating numbers of samples, selecting
among them, making incremental improvements and hybrid samples, again
evaluating the results, and so on. This manual practice is quite reminiscent of
the evolutionary process of genetic variation and natural selection.
It was seemingly inevitable that soon after the
adoption of the computer by designers as a manual tool for CAD, there would
follow the adoption of genetically inspired algorithms for the creation and
selection of variations. In fact the
generative artist William Latham initially used an evolutionary system that
existed purely on paper, and only later did he move to computerized versions.
[6]
Clearly any attempt to define generative art would
have to include all of the above, as there is no obvious reason to privilege
one form of contemporary generative art practice over another. And few would want to stop with just the
above. One could also include, for
example, robot art and math art as clusters of generative art activity.
The fine arts offer a number of challenges in this
regard. For example, in the 20th
century a number of artists such as John Cage, William Burroughs, and Marcel
Duchamp embraced randomization as a fecund generative principle. Minimalists such as Carl Andre, Mel Bochner,
and Paul Morgenson used simple mathematical principles to generate
compositions. The conceptual artist Sol
Lewitt uses combinatorial systems to create complex works from simple
components, and conceptual artist Hans Haacke explored physical generative
systems in his early work.
And indeed some have wondered whether a painter
like Kenneth Noland should be considered a generative artist given his
“systemic art” practice, or whether Jackson Pollock's drip and splash method
qualifies as the kind of randomization that would place his work in the realm of
generative art. I, in fact, don't
consider Noland and Pollock to be generative artists. But given the dizzying variety generative art offers it is an
entirely legitimate question to ask
2.1 From the Top Down – Generative Art Considered Literally
The term generative art can also be explored from the
top down by considering its literal abstract meaning.
I often joke with my students that it is easy to tell
if something is generative art. First
it must be art, and second it must be generative. The joke here is, of course, I am begging the question. One difficult question is replaced by two
difficult questions. What do we mean by
art, and what do we mean by generative?
The "what is art?" question is often brought
up to mock and sound a cautionary note about the perils of intellectual
discourse rather than to pose a serious question. But this is mostly unfair.
The discussion spawned by the question "what is art?" can in
fact be productive and useful. It has
perhaps been best considered by specialists in aesthetics in the analytic
school of philosophy found primarily in the U.S. and U.K. A recounting of this debate is beyond the
scope of this paper but is well-summarized elsewhere, for example Carrol’s book
“Philosophy of Art”. [7]
Viable contemporary definitions of art generally
include a notion akin to fuzzy set theory so that some things may be considered
more fully art than others. In a similar way we can expect that some works are
more fully generative art than others.
In addition current notions about art recognize it as a social and
historical notion that changes over time.
To the extent generative art is art surely this must apply there as
well. But I hope to show that the
generative aspect can be fixed in a more stable way.
The word "generative" simply directs
attention to a subset of art, a subset where potentially multiple results can
be produced by using some kind of generating system.
It is important to note here that if generative art also included art produced by any kind of generating idea, then generative art would include all art, and it would loose its utility as a distinct term.
3. Generative Art Defined
So a useful definition of generative art should (1)
include known clusters of past and current generative art activity, (2) allow
for yet to be discovered forms of generative art, (3) exist as a subset of all
art while allowing that the definition of "art" can be contested, and
(4) be restrictive enough that not all art is generative art.
Whether considered from the top down or the bottom up,
the defining aspect of generative art seems to be the use of an autonomous
system for art making. Here is the
definition I've been using in my class:
Generative art refers to any art practice where the artist uses a system, such as a set of natural language rules, a computer program, a machine, or other procedural invention, which is set into motion with some degree of autonomy contributing to or resulting in a completed work of art.
The key element in generative art is then the system to which the artist
cedes partial or total subsequent control.
And with this definition some related art theory questions come quickly
to mind. A hint as to how that conversation
might go will be offered at the end of this paper.
For now here are some observations about this definition. First, note that the term generative art is
simply a reference to how the art is made, and it makes no claims as to why the
art is made this way or what its content is.
Second, generative art is uncoupled from any particular technology. Generative art may or may not be “high
tech”. Third, a system that moves an
art practice into the realm of generative art must be well defined and self-contained
enough to operate autonomously.
So if systems are in a sense the defining aspect of generative art, it is worth asking if all systems alike, or if there is a useful way to sort them out and thus, by implication, sort out various kinds of generative art. This is the topic of the next few sections.
4. Complexity Science as a Context for Understanding Systems
Over the last 20 years or so scientists have attempted
to create a new understanding of systems.
Under the general rubric of "complexity science" and
“complexity theory” various systems, and various kinds of systems, have been
studied, compared, contrasted, and mathematically and computationally
modeled. An abstract understanding of
systems is beginning to emerge, and given that systems are a defining aspect of
generative art, complexity science has much to offer the generative
artist. And indeed a great deal of the
work presented at this very conference in past years is, explicitly or
implicitly, rooted in complexity science.
Science generally proceeds in a reductive manner, the
thinking being that by breaking down complicated phenomena into its figurative
(or literal) atomic parts one gains predictive and explanatory power. The problem with reductionism, however, is
that it is often difficult to put the pieces back together again.
This is especially true of complex systems. When scientists speak of complex systems
they don't mean systems that are complicated or perplexing in an informal
way. The phrase "complex
system" has been adopted as a specific technical term. Complex systems typically have a large
number of small parts or components that interact with similar nearby parts and
components. These local interactions
often lead to the system organizing itself without any master control or
external agent being "in charge".
Such systems are often referred to as being self-organizing. These self-organized systems are also
dynamic systems under constant change, and short of death or destruction, they
do not settle info a final stable "equilibrium" state. To the extent these systems react to changes
in their environment so as to maintain their integrity, they are known as
complex adaptive systems.
In common
language one is reminded of the saying that “the whole is greater than the sum
of its parts.” Local components will interact in “nonlinear” ways, meaning that
the interactions do more than merely add up…they exponentiate. Examples of
complex systems are familiar to everyone.
The weather, for example, forms coherent patterns such as thunderstorms,
tornados, and hot and cold fronts, yet there is no central mechanism or control
that creates such patterns. Weather
patterns “emerge” all over and all at once.
In the near term weather can be predicted with some accuracy, but beyond
more than a few days the weather becomes quite unpredictable.
The stock market
is similarly a complex system with emergent properties. Billions of shares and transactions are
linked in a finite chain of cause and effect, and patterns such as booms and
busts emerge from the overall system.
Yet no one factor dominates or “plans” the market, and even with all of
the relevant information available to the public, the stock market generates
surprising and unpredictable behavior.
Additional
examples of complex systems include the brain (as studied by biologists) and
the mind (as studied by psychologists), the predation and population cycles of
animals in an ecosystem, the competition of genes and resulting evolution of a
given species, and the rise and fall of cultures and empires. Each of these systems consists of many
components (such as cells, chromosomes, citizens, etc.) that interact with
other nearby components, and form a coherent pattern or entity without any
central control or plan as to how that should happen.
Thus complex systems often develop in ways that are dramatic, fecund,
catastrophic, or so unpredictable as to seem random. Complexity science is a relatively new, and at times
controversial, attempt to understand such systems by bridging a number of
traditionally distinct disciplines. The
ambition is to understand the commonalities systems exhibit across all scales
and hierarchies.
Note that the study of complex systems also provides context and perspective for understanding simple systems. And the notion of generative art offered here includes both complex and simple systems.
5. Chaotic Systems and Random Systems
Generative artists often use randomization. Complexity scientists often speak of
chaos. In many cases a chaotic system
may seem random because its behavior is so unpredictable. But it is important to keep in mind that
there is a difference.
Complex systems often include chaotic behavior, which
is to say that the dynamics of these systems are nonlinear and difficult to
predict over time, even while the systems themselves are deterministic machines
following a strict sequence of cause and effect. The nonlinearity of chaotic systems results in the amplification
of small differences, and this is what makes them increasingly difficult to
predict over time. This is usually
referred to as sensitivity to initial conditions or "the butterfly
effect", from the notion that a butterfly flapping its wings in Hawaii can
result in a tornado in Texas. [8]
It is important to remember, especially within the
context of generative art, that chaotic systems are not random systems. Natural chaotic systems may be difficult to
predict but they will still exhibit structure that is different than purely
random systems.
For example, even though it is difficult to predict
the specific weather 6 months from now, we can be relatively sure it won't be
200 degrees outside, nor will we be getting 30 feet of rain on a single day,
and so on. The weather exists within
some minimum and maximum limits, and those expectations are a sort of container
for all possible weather states. This is what scientists call the phase space,
and it describes a sort of consistent general shape the chaotic system
eventually traces out even though it remains unpredictable in precise detail.
What about day to day weather transitions? The best predictor of tomorrow’s weather is
today’s weather. Even in my hometown of
Chicago, known for its crazy weather, a cold day is usually followed by another
cold day. And a hot day is typically
followed by a hot day. And so on. The
transition from one weather state to another can be thought of as a path within
the state space. Those paths are
continuous (no instantaneous jumps are allowed) and exhibit this form of local
auto-correlation. In other words unlike
purely random systems chaotic systems have a sense of history.
I find life to be more like a complex chaotic system
and less like a simple random one.
There is uncertainty, but there is still a sense that cause and effect
are at play. I may not be able to make
a specific prediction for a specific time, but I can know how things tend to
go. And I can often consider some
things as impossibilities. There are surprises, but not at every single turn
because there are also correspondences.
In a related way, artificial chaotic systems seem more like nature, and more like real life, than artificial random systems. There is likely a lesson there for generative artists.
6. Notions of Order and Disorder in Information Theory
While we have an
intuitive sense of what we mean when we refer to a system as "simple"
or "complex" developing a formal technical measure of complexity that
corresponds well to our intuitive sense is not easy.
An earlier
related attempt to better understand communication systems was initiated by
Claude Shannon in the form of information theory. [9] For the purposes of
analyzing the capacity of a given communication channel, the core idea is that
the more "surprise" a given communication can exhibit the more
information it contains.
For example,
consider a channel that can only send the letter "A" at regular
intervals.
A
A A A A A A A A A A A A A A A A A A A A
Every
transmission is the same and allows for no modulation of the signal. It is, in a sense, a highly ordered signal
to the extreme. But even more, if all a channel can carry is the letter
"A" there are no surprises, and thus no information can be
transmitted.
A channel that
allows the sending of English language words like so:
I L I K E
G E N E R A T I V E A R T
contains
variation from character to character, and thus allows information to
flow. It should be noted that
information theory is not fundamentally about the transmission of meaning, but
rather the capacity to transmit symbols.
The following nonsense sentence sent via the same channel:
P
A P E R B I G W O R K
I C A T S
is about the same
amount of information even though it is meaningless.
Natural language
contains redundancy, which is another way of saying that the text has
consistent patterns, such as statistical frequencies of letter combinations
that can potentially be compressed out.
For example, since we can anticipate the structure of the English
language we might send the following compressed string with relative success:
I L I K
G E N A R T
In the limiting
case a signal in a channel that sends random letters is at maximum
information. For example:
F O E V Q K M V K D Y P Q X C I H R S N W
A truly random
stream of characters is maximally disordered and has no underlying
structure. Thus there are no patterns
and redundancy to take advantage of, and no compression is possible.
While saying a
highly ordered sting of repeating characters has low information seems
intuitively correct, saying a highly disordered string of random characters has
maximum information seems peculiar. In
terms of our human ability to extract meaning from a given experience we
require a mix of surprise and redundancy, i.e. a signal somewhere between
extreme order and disorder.
In his 1958 book
"Information Theory and Esthetic Perception" Abraham Moles applies
these notions, along with findings from the realm of perceptual psychology, to
analyze the arts. [10] In line with the above, he attempts to apply various
statistical measures to classify musical works on a spectrum from
"banal" to "novel" corresponding to the relative order
versus disorder of the given information.
And indeed one can easily intuit that forms such as, for example,
traditional folk music are more ordered and banal than, say, free jazz which
encourages more disorder and novelty.
At the extremes,
however, highly ordered music (e.g. playing the same note over and over again)
is of no greater intrinsic aesthetic interest than highly disordered music
(e.g. playing entirely random pitches and durations). In terms of the pure esthetics we will quickly lose interest in
both. (Such performances might,
however, be perfectly legitimate given an appropriate conceptual framework
providing context and thus meaning).
Working artists understand that an audience will quickly tire of both a highly ordered and a highly disordered aesthetic experience because both lack any structural complexity worthy of their continued attention. The intuition that structure and complexity increase somewhere between the extremes of order and disorder leads us to the consideration of "effective complexity".
7. Algorithmic Complexity and Effective Complexity
Complex systems
stand in contrast to simple systems, and attempts have been made to invent
measures that quantify the relative complexity of given systems. One approach is to consider the algorithmic
complexity (AC) of a given system.
Algorithmic complexity is also called the algorithmic information
content (AIC), and was independently developed by Kolmogorov, Solomonoff, and
Chaitin.
It is known that in
principle any system can be mapped into a smallest possible program running
on a universal computing machine generating a growing string as output over
time. Some systems, such as fractals,
require infinite time to generate because they have infinite detail. But that is not to say that fractals have
infinite complexity. They are simple in
the sense that they exhibit self-similar structure at every scale. And, in fact, a fractal algorithm can be
very compact indeed. [11]
One might hope
that AC or AIC is a good candidate for a measure of what we intuitively
consider complexity. Perhaps the larger
the algorithmic complexity the more complex the system.
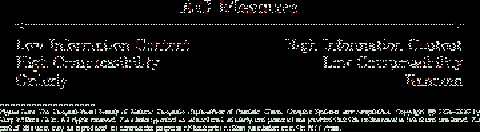
Figure 7.1
Unfortunately, in
the case of random processes we run into the same paradox as we see in
information theory.
For our low
information example the AIC would be very small, and independent of string
length, because the algorithm could be very small. For example:
loop: print "A"
go to loop
For our
intermediate information, English language, example the AIC would be a bit
larger. The redundancy of natural
language allows the use of an algorithm that carries a compressed version of
the string and then expands it. For example
the algorithm:
print( expand( "NIFNEPOLDFIMDMEUMN" ) )
might result in the string:
HERE IS THE MESSAGE AFTER IT HAS BEEN UNCOMPRESSED
Unfortunately in
the case of a system that generates a purely random result the AIC will be
quite a bit larger. Without redundant
information in the string, in other words without structure, no further
lossless compression is possible. The
smallest algorithm would be a program that is a single "print"
statement that includes the literal string in question. Thus for a random string the AIC is at least
as long as the length of the string.
print("APFUYWMVPBXTWLFMCRORNBHTEIYBCMIBUNEPMVU")
Similar to what
was previously shown, the AIC becomes larger the more random the message is,
and this conflicts with our intuitive sense of complexity. As Murray Gell-Mann, one of the founders of
the Sante Fe Institute and complexity science, puts it:
"This property of AIC, which leads to its being
called, on occasion,
"algorithmic randomness,” reveals the
unsuitability of the quantity as
a measure of complexity, since the works of Shakespeare have a
Lower AIC than random gibberish of the same length
that would
typically be typed by the proverbial roomful of
monkeys."
What is needed is
a measure of "effective complexity" (EC) such that systems that are
highly ordered or disordered are given a low score, indicating simplicity, and
systems that are some where in between are given a high score, indicating
complexity, Gell-Mann goes on to say:
"A measure that corresponds much better to what
is usually meant by
complexity in ordinary conversation, as well as in
scientific discourse,
refers not to the length of the most concise
description of an entity
(which is roughly
what AIC is),
but to the length of
a concise
description
of a set of the
entity's regularities. Thus something
almost entirely random, with practically no
regularities, would have
effective complexity near zero. So would something completely
regular, such as a bit string consisting entirely of
zeroes. Effective
complexity can be high only a region intermediate
between total
order and complete disorder"
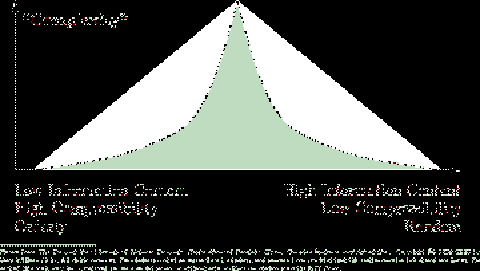
Figure 7.2
To measure EC Gell-Mann proposes to
split a given system into two algorithmic terms, with the first algorithm
capturing structure and the second algorithm capturing random deviation. The EC would then be proportional to the
size of the optimally compressed first algorithm that captures structure. There are objections to this approach, for
example some maintain that this notion of structure is subjective and remains
in the eye of the beholder. And indeed
there are competing proposals as to the specifics of effective complexity. [12]
The important point for the purpose of this paper is that complexity science has produced a robust general paradigm for understanding and classifying systems. Systems exist on a continuum from the highly ordered to the highly disordered. Both highly ordered and highly disordered systems are simple. Complex systems exhibit a mix of order and disorder.
8. Generative Art Systems in the Context of Complexity Theory
Earlier I offered
a definition of generative art where the key is the use of systems as an
indirect production method. This, taken
in combination with the new paradigm for systems suggested by complexity
science, results in a paradigm for understanding and sorting though generative
art systems.
This paradigm for
generative art systems is captured in the following figure, a variation on the
previous figures from Gary Flakes wonderful book "the Computational Beauty
of Nature". [13]
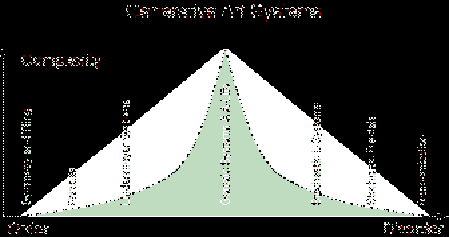
Figure 8.1
First one should
note that complexity is specific to a given system, and the classifications
shown here are generalities. Not all
genetically inspired evolutionary systems are going to be equally complex. Some L-systems are going to be more ordered
than others, and some stochastic L-systems are going to be more disordered than
others. Also some L-systems are
equivalent to fractals, while others using parametric and contextual mechanisms
are more complex (as shown). [5]
But if we accept
this paradigm, that generative art is defined by the use of systems, and that
systems can be best understood in the context of complexity theory, we are lead
to an unusually broad and inclusive understanding of what generative art really
is.
And while it shouldn't be terribly surprising that the
earliest forms of generative art used simple systems, some will find it
surprising and perhaps even controversial that generative art is as old as art
itself.
8.1 Highly Ordered Generative Art (and Generative Art as Old as Art Itself)
In every time and
place for which we can find artifacts, we find examples of the use of symmetry
in the creation of art. Reasonable
people can disagree as to at what point the use of symmetry can be considered
an autonomous system. But even among
the most so called primitive peoples examples abound in terms of the use of
geometric patterns in textiles, symmetric designs about a point, repeating
border designs, and so on. Many of
these are well documented in books by authors like Hargittai and Hargittai [14]
and Stevens. [15]
The artistic use
of tiling, in particular, is nothing less than the application of abstract
systems to decorate specific surfaces.
Leading the most notable examples in this regard are perhaps the
masterworks found in the Islamic world. It is no coincidence the Islamic world also provided one of the
significant cradles of mathematical innovation. It is also worth noting that the word "algorithm" has
its roots in the Islamic world.
Highly ordered
systems in generative art also made their appearance in innovative 20th
century art. A popular contemporary
tile artist, and student of the Islamic roots, is M. C. Escher. While lacking in formal mathematical
training, it is clear that he had a significant understanding of the generative
nature of what he called "the regular division of the plane". Without the use of computers he invented and
applied what can only be called algorithms in the service of art. [16]
In addition,
minimal and conceptual artists such as Carl Andre, Mel Bochner, Donald Judd,
Paul Mogenson, Robert Smithson, and Sol Lewitt used various simple highly
ordered geometric, number sequence, and combinatorial systems as generative
elements in their work. [17] [18]
In my class I
frequently remind my students that you don't need a computer to create
generative art, and that in fact generative art existed long before
computers. With tongue only partially
in cheek I also sometimes comment that generative art lead to the invention of
the computer!
A highlight in
the history of generative art was the invention of the Jacquard loom. Manual textile machines long allowed weavers
to apply repetitive formulas in the creation of patterned fabrics. With the industrial revolution some of these
systems were automated, but it was Jacquard's 1805 invention that introduced
the notion of a stored program in the form of punched cards that revolutionized
the generative art of weaving.
Interestingly one of Jacquards primary goals was to allow the automation
of patterns of greater complexity. Later
both Charles Babbage and Charles Hollerith leveraged Jacquard's method of punch
card programming in their efforts to invent the computer.
But is generative
art really as old as art? Many are
familiar with the discoveries of representational cave paintings some 35,000
years old that depict animals and early mans daily life. But in 1999 and 2000 a team led by
archaeologist Christopher Henshilwood of the South African Museum in Cape Town
uncovered the oldest known art artifacts. Etched in hand sized pieces of red
ochre more than 70,000 years old is an unmistakable grid design made of
triangular tiles that would be clearly recognizable as such to Escher or
generations of Islamic artists.
While the
etchings, like all ancient archaeological finds, are not without controversy,
many find them compelling examples of abstract geometric thinking with an
artistic response. In a related article
in Science anthropologist Stanley Ambrose of the University of Illinois, Urbana-Champaign
says "This is clearly an intentionally incised abstract geometric
design...It is art." [19]
Obviously two stone etchings alone cannot make the
case that generative art is as old as art itself. But around the world, and though out history, there is
overwhelming evidence of artists turning to systems of iterative symmetry and
geometry to generate form. Early
generative art may seem unsophisticated because it is highly ordered and
simple, but our complexity inspired paradigm for generative art has an
important place for highly ordered simple systems
8.2 Highly Disordered Generative Art
The first use of randomization in the arts that I am aware of is an
invention by Wolfgang Amadeus Mozart.
Mozart provides 176 measures of prepared music and a grid that maps the
throw of a pair of dice, and a sequence number (first throw, second throw, etc)
into the numbers 1 through 176. The
player creates a composition by making a sequence of random dice throws, and
assembling the corresponding measures in a sequential score. Perhaps Mozart knew intuitively that purely
random music isn’t terribly interesting because he found a primitive way to mix
order and disorder. The short
pre-composed measures provide order, and the throw of the dice provide
disorder.
Randomization in the arts came into its own primarily in the 20th
century. As a young artist Elsworth
Kelly used inexpensive materials such as children’s construction paper along
with chance methods to create colorful collages. He was inspired to do this after observing the random patchworks
that would develop in the repair of cabana tents on the French Rivera. [20]
The writer William Burroughs famously used his Dada inspired “cut-up”
technique to randomize creative writing.
Less well known are Burroughs experiments in visual art using shotgun
blasts to randomly scatter paint on, and partially destroy, plywood
supports. [21]
Occasionally Carl Andre would use a random spill technique rather than
his more typical highly ordered assembly system. [18]
Certainly one of the most famous advocates for the random selection of
sounds in music was John Cage.
In the era of computer-generated art the use of pseudo-random number
generators becomes perhaps the most popular digital generative technique.
As mentioned earlier, generative art is a long-standing art practice,
but different artists may choose the same generative technique for wholly
different reasons. For John Cage the
motivation for randomization was a Zen inspired acceptance of all sounds as
being equally worthy. For Andre the
intent was to somewhat similarly focus attention on the materials, but also to
assault art-world expectations regarding composition. For many contemporary electronic musicians performing in a club
context the use of randomization isn’t so theory laden. It’s simply an attempt to add an element of
surprise to make things more interesting.
It is important to remember that what
generative artists have in common is how they make their work, but not why they
make their work, or even why they choose to use generative systems in their art
practice. The big tent of generative
art contains a diversity of intent and opinion.
8.3 Complex Generative Art
One need only survey
the proceedings of this very conference to see that the bulk of those working
on the cutting edge of generative art are working with systems that combine
order and disorder. These artists are
exploring many of the same systems that are the very meat of complexity
science. Examples include genetic algorithms, swarming
behavior, parallel computational agents, neural networks, cellular automata,
L-systems, chaos, dynamical mechanics, fractals, a-life, reaction-diffusion
systems, emergent behavior, and all manner of complex adaptive systems. It would be difficult to summarize all of
this work in a single paper, and indeed there is no need to here.
The point I would like to emphasize here is that while complex systems dominate our current attention, and in many ways represent the future of generative art, complex systems are not “better than” simple systems. Each has a historical and contemporary place in art practice. Both the ordered and the disordered, and the simple and the complex, are needed to complete an account of systems, and to complete an account of generative art.
9. Complexity Theory as a Context for Generative Art Theory
It is my hope that bolstered by the view of systems that complexity
theory provides, a fecund context for generative art theory will result from a
broad and inclusive systems oriented definition of generative art. Towards that end I will close by raising
some common questions I hear regarding generative art. While some initial answers are provided
here, my primary intent is to suggest that the paradigm suggested in this paper
is an inviting context further discussion.
9.1 Is generative art a subset of computer art?
Because contemporary generative art is so very often computer based many
assume it is a subset of computer art.
I’ve tried to show here that generative art preceded computer art, and
in fact is as old as art itself. Equally important is the virtual certainty
that new forms of generative art will come after the computer as well. Nanotechnology, genetic engineering,
robotics, and other technologies will no doubt offer generative artists some
wonderful opportunities.
9.2 Isn’t generative art a subset of abstract art?
Generative art refers to a way to create art rather than an art
style. Consider the work of Harold
Cohen who creates software that autonomously designs stylized representational
works depicting people in lush tropical settings. [22] And of course there is the growing use of
genetic and other generative systems in the design of practical and decorative
objects.
9.3 How can handmade art be generative?
A given work being generative is a matter of degree, i.e. generative art
is a fuzzy set. Generative art practice
is really the key, and a given work might be created only partially via the use
of an autonomous system. In principle
any computer based generative method could be carried out by hand. More practically, if an artist creates a
system and then hands it off to an artisan for use in laying tiles, how
different is that from using a generative art robot? And how different is that from the artist choosing to do it
himself? What is key is that a system is
applied with some degree of autonomy, whether or not the construction happens
by hand. Handmade generative art is
still quite different than other handmade art where the artist is making
intuitive design judgments from one moment to the next throughout the entire
construction process.
9.4 Why do artists choose to work using generative methods?
Generative art is a method of making art, but it carries with it no
particular motivation or ideology. In
fact the use of generative methods may have nothing to do with the content of
the work at all. For example,
filmmakers may use generative methods to synthesize imagery for purely economic
reasons. At the other extreme some generative
artists create works where there is no distance at all between the generative
production method and the meaning of the work.
These are generative artists exploring systems for their own sake. And of course there are numerous artists
somewhere in between. There are as many
reasons to use generative methods as there are generative artists. Perhaps more.
9.5 Is generative art an art movement?
Generative art as described here is simply systems oriented art
practice, and it has roots in the oldest known art. Various generative systems have been used by those in assorted
art movements over the years.
Generative art as a systems oriented art practice is much too large to
be claimed by any single art movement.
There is, however, an earlier and somewhat obscure use of the same
phrase in the context of a specific art movement. Our discussion here should not be confused with this narrow art
historical technical homonym.
“Generative Art - A form of geometrical abstraction in which a basic element is made to ‘ generate' other forms by rotation, etc. of the initial form in such a way as to give rise to an intricate design as the new forms touch each other, overlap, recede or advance with complicated variations. A lecture on 'Generative Art Forms' was given at the Queen's University, Belfast Festival in 1972 by the Romanian sculptor Neagu, who also founded a Generative Art Group. Generative art was also practiced among others by Eduardo McEntyre and Miguel Ángel Vidal [1928- ] in the Argentine."[23]
This same source also defines “Systemic Art” which is at times confused
with our contemporary understanding of generative art.
"Systemic Art – a term
originated by the critic Lawrence Alloway in 1966 when he organized an
exhibition 'Systemic Painting' at the Solomon R. Guggenheim Museum, New York,
to refer to a type of abstract art characterized by the use of very simple
standardized forms, usually geometric in character, either in a single
concentrated image or repeated in a system arranged according to a clearly
visible principle of organization. The Chevron
paintings of Noland are examples of Systemic art. It has been described as a branch of Minimal art, but Alloway
extended the term to cover Colour Field painting." "[23]
9.6 Isn’t generative art about the issue of authorship?
Certainly when one turns the creation of a work of art over to a
machine, and part of the work is created without the participation of human
intuition, some will see a resonance with contemporary post-structural
thinking. Some generative artists work
specifically in the vein of problematizing traditional notions about
authorship. But the generative approach
has no particular content bias, and generative artists are free to explore
life, death, love, war, beauty, or any other theme.
9.7 Was Jackson Pollock a generative artist?
Partially because Jackson Pollock’s best-known work seems “random”, and
partially because his “drip and splash” technique seems to be a retreat from
conscious artistic control, many wonder whether Jackson Pollock can be
considered a generative artist. I don’t
consider his work to be generative art because there is no autonomous system
involved in the creation of his paintings.
There is, however, an interesting link between Pollock’s most famous
work and complexity theory. Physicist
Richard Taylor has shown that Pollock’s drip and splash marks are fractal in
nature, that they are likely the result of Pollock learning how to “launch” the
paint with his wrist and arm so as to induce chaotic fluid flow, and that as
Pollock’s work progressed he was able to achieve higher and higher degrees of
fractal dimension. [24]
Perhaps it is this fractal look that encourages the knowledgeable
observer to try to connect Pollock to generative art. In any case Pollock applied the paint manually without the use of
any external system. The work was a
hard earned intuitive creation requiring physical discipline, and requiring
many sessions and constant reworking.
However, the fact that his manual practice rests on underlying physics
that happens to engage contemporary notions of fractals and chaos theory
shouldn’t sway one to think of these paintings as generative works. All artwork has underlying physics, and if
that were the measure then all art would have to be called generative art.
9.8 Is Hans Haacke a generative artist?
Han’s Haacke is a prescient artist whose
work critiques both physical and social systems in a bold way that precedes by
decades the similar attempts now underway in complexity science. It is
important, however, to differentiate between works that are about systems and
works that use systems in their creation.
Haacke has produced both.
As curators for the exhibit “COMPLEXITY –
Art and Complex Systems” Ellen K. Levy and I were thrilled to be able to
present Haacke’s 1963 piece “Condensation Cube”. A simple acrylic cube with a bit of water at the bottom and
sealed shut, “Condensation Cube” becomes a miniature weather system as an ever
changing display of condensation forms on the cube’s walls. This work anticipated meteorologist Ralph
Lorenz’s discovery of chaotic strange attractors, and stands as a wonderful
example of generative art. [25]
The following artists statement written
by Haacke in 1965 could stand today as a manifesto for generative artists
exploring complex adaptive systems.
HANS
HAACKE Statement
...make something which
experiences, reacts to its environment, changes, is non-stable...
...make something
indeterminate, which always looks different, the shape of which cannot be
predicted precisely...
...make something which
cannot 'perform' without the assistance of its environment...
...make something which
reacts to light and temperature changes, is subject to air currents and
depends, in its functioning, on the forces of gravity...
...make something which
the 'spectator' handles, with which he plays and thus animates...
...make something which
lives in time and makes the 'spectator' experience time...
...articulate: something
natural...
Cologne, January 1965 [26]
9.9 Is Sol Lewitt a generative artist?
Most of Sol Lewitt’s work is generative, and as a conceptual artist much
of his attention is focused on exploring systems for their own intrinsic
value. In his “Paragraphs on Conceptual
Art” from 1967 he says, “The idea becomes a machine that makes the art” and
refers to the actual construction of the work as “a perfunctory affair”. His combinatorial drawings and sculptures
demonstrate the continuing viability of highly ordered systems in generative
art.
9.10 Shouldn’t all generative art exhibit constant change and unforeseeable results?
There is much to be said for the creation of complex systems as
installation art that exhibits dynamics in real time for an audience. It is a wonderful way for an artist to share
his explorations of complex systems, and especially complex adaptive systems,
with an audience. However, an art practice
that uses a dynamic complex system to create what is ultimately a static object
or recording is still generative art.
As is, for that matter, works resulting from the use of simple
generative methods.
9.11 Is generative art modern or post-modern?
Generative art is ideologically neutral. It is simply a way of creating art and any
content considerations are up to the given artist. And besides, generative art historically precedes modernism,
post-modernism, and just about any other “ism” on record.
Certainly one can make generative art that exhibits a
postmodern attitude. Many do. But one can also make generative art that
attempts to refute post-modernism.
Two of the most significant impacts of post-modernism
on art are (1) the proposed abandonment of formalism and beauty as a meaningful
area of exploration, and (2) the proposed abandonment of the notion that art
can reveal truth in any non-relativistic way. Form, beauty, and knowledge are
held to be mere social constructions.
Generative art can be used to attack these fundamental
points head on. First, generative
artists can explore form as something other than arbitrary social
convention. Using complex systems artists
can create form that emerges as the result of naturally occurring processes
beyond the influence of culture and man.
Second, having done this, generative artists can
demonstrate by compelling example reasons to maintain faith in our ability to
understand our world. The generative
artist can remind us that the universe itself is a generative system. And through generative art we can regain our
sense of place and participation in that universe.
References
[1] Galanter, P. Foundations
of generative art systems – a hybrid survey and studio class for graduate
students. Generative Art 2001: Proceedings of the 4th
International Conference. Generative Design Lab, Milan Polytechnic, Milan 2001
[2] Schwanauer, S. M. and D. A. Levitt
(1993). Machine
models of music . Cambridge, Mass., MIT Press.
[3]
Miller, Dennis, Game of Chance,
Electronic Musician, p 53-64, November 2003
[4] Perlin, Ken. An
Image Synthesizer, Proc. SIGGRAPH '85, ACM Computer Graphics, Vol.19, No.3,
pp.287-296.
[5] Prusinkiewicz, P., A. Lindenmayer, et al. (1990). The algorithmic beauty
of plants . New York, Springer-Verlag.
[6]
Todd, S., Latham, W. (1992) Evolutionary art and computers. London, Academic
Press Limited
[7]
Carrol, Noel. (1999) Philosophy of Art, London, Routledge
[8]
Casti, John L. (1994) Complexification,
New York, HarperCollins
[9] Shannon, Claude E. A
mathematical theory of communication. The Bell System Technical Journal,
27(3):379--423, 1948.
[10] Moles,
A. A. (1966). Information theory and esthetic perception. Urbana, University of
Illinois Press.
[11]
Bar-Yam, Y. (1997). Dynamics of complex systems. Reading, Mass.,
Addison-Wesley.
[12] Gell-Mann, Murry. What is complexity? Complexity – John Whiley and
Sons, Vol 1 No 1, 1995
[13]
Flake, G. W. (1998) The computational beauty of nature, Cambridge, The MIT
Press
[14]
Hargittai, I., Hargittai, M. (1994) Symmetry: a unifying concept, Bolinas CA,
Shelter Publications
[15]
Stevens, P. S. (1981). Handbook of regular patterns: an introduction to
symmetry in two dimensions. Cambridge, Mass., MIT Press.
[16] Locher, J. L., ed. (1992) M. C. Escher: His
life and complete graphic work, New York, Abradale Press
[17]
Alberro, A. and B. Stimson, ed. (1999). Conceptual
art: a critical anthology. Cambridge,
Mass., MIT Press.
[18]
Meyer, J. (2000) Minimalism: themes and movements. London, Phaidon
[19]
Balter, Michael. Oldest Art – From a
Modern Human’s Brow - or Doodling. Science, Vol. 295 pp 247-249
[20] Bois, Y. A., J. Cowart, et al. (1992).
Ellsworth Kelly: the years in France, 1948-1954 . Washington, D.C. [München],
National Gallery of Art; Prestel-Verlag.
[21]
Sobieszek, R. A. and W. S. Burroughs (1996). Ports of entry: William S.
Burroughs and the arts . Los Angeles New York, Los Angeles County Museum of Art
; Distributed in the USA by Thames and Hudson.
[22]
McCorduck, P. (1991). Aaron's code: meta-art, artificial intelligence, and the
work of Harold Cohen . New York, W.H. Freeman
[23]
Osborne, Harold, ed. (1988) The Oxford Companion to Twentieth-Century Art.
Oxford, Oxford University Press
[24] Taylor, R., Micolich, A., Jones, D. The constructtion of Jackson Pollock’s
fractal drip paintings. Leonardo, Vol 35, No. 2, pp. 203-207
[25]
Benthall, J. (1972). Science and technology in art today. New York,, Praeger
[26]
Cotter, S., Douglas, C. ed. (2000) Force fields: phases of the kinetic.
Barcelona, Museu d’Art Contemporani de Barcelona