What is Emergence?
Generative Murals as Experiments in the Philosophy of Complexity
Philip
Galanter, BA, MFA
Arts Technology Group, New York University, New
York, USA.
e-mail: galanter@nyu.edu.
Abstract
The
Traveling Salesman s a series of site specific wall paintings based on a canonical
optimization problem. Well known among computer scientists, the Traveling
Salesman Problem (TSP) is a search for the shortest path visiting a number of
locations exactly once. For this piece
software is used to solve the problem for sets of random points, and then each
optimized path is transformed into an image.
The resulting images exhibit a consistent style that is simultaneously
random yet visually coherent. Some would
call this emergent form.
But emergence is a hotly disputed term from the field of complexity
science and the philosophy of science.
Complexity Science studies systems made up of large numbers of
interacting parts which often exhibit order in the midst of nonlinear,
feedback, and/or chaotic mechanisms.
These so-called "emergent behaviors" are not typically
explained or predicted by sciences traditional reductionist methods. Complexity science, in part, seeks to
explain emergence.
The
Traveling Salesman explores the ontological and epistemological aspects of the
question "what is emergence"?
1. The Traveling Salesman
One
day while developing my "Foundations of Generative Art Systems" [1]
class I was looking for a good example to illustrate the use of genetic
algorithms. I came acoss an article by
Larry Fogel [2] documenting his early use of genetic algorithms to solve The
Traveling Salesman Problem.
The
Traveling Salesman Problem, or TSP, is well-known among computer scientists,
mathematicians, engineers and others.
The problem is easy to state. A
salesman has to visit a number of cities exactly once, and the goal is to find
the tour that minimizes the total distance traveled. (There are other variations as well). [3]
The
TSP is of interest in part because it represents a broad range of applications
including all manner of transportation logistics, but it also maps into less
obvious applications such as genome sequencing, integrated circuit design,
computer network design, and power grid design.
The
TSP is also of interest because it is a combinatorial problem thought to be
NP-Complete. Informally NP-Complete
problems are those which become exponentially more difficult to solve as their
complexity is increased linearly. For
example, if a 200 city problem takes 1 second for a computer to solve, a 400
city problem might take 4 seconds to solve, and an 800 city problem might take
16 seconds to solve. Interestingly if a
TSP algorithm could be found that only requires a linear increase in
computation time, it would generalize to a linear solution for all NP-Complete
combinatorial problems. It is thought,
however, that such a solution is an impossibility.
In
practice the most efficient algorithms for the TSP are not genetically
based. But because the problem is easy
to understand it can nevertheless be useful in a teaching context. In a typical implementation each genotype is
in fact a proposed solution to the problem, i.e. a tour. At each step the phenotype, the total
distance traveled, is evaluated. Very
long tours are eliminated from the gene pool, and the genes for short tours are
allowed to continue breeding. Because viable genes must be a cycle that
includes each city once and only once, typical simple mutation and crossover
operations are usually avoided. Instead
similar operations that ensure legal tours are used. After a number of generations the solutions in the gene pool
improve and perhaps ultimately yield an optimal tour, i.e. the shortest
possible path.
Here
is the graph Fogel originally published in his groundbreaking work. He first generated a set of random points
(i.e. “cities”) and then used genetically inspired software to generate this
TSP solution.
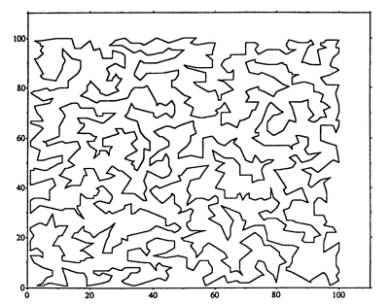
Figure 1.0
As
I viewed this graph something strange happened. I stopped thinking about the lesson I was preparing and the
various technical aspects of genetic algorithms. I was lost in the appreciation
of the esthetics of what could be viewed as a line drawing. The formal aspects of this would-be machine
drawing seemed to exhibit an intelligence and coherence that had nothing to do
with combinatorial analysis and optimization.
A set of random points had been transformed into a compelling image with
a definite style. I wondered if an
artist, if asked to connect the dots, could come up with an equally satisfying
line drawing.
It
seemed as if formal beauty was an emergent property arising out of the
complexity of genetic competition. With
the aid of a scanner and Photoshop I appropriated the graph and added some
color to help emphasize the overall contours of the “drawing” resulting in the
following image.

Figure 1.1
Those
studying complex systems are not unanimous as to how to define complexity, but
virtually all would agree that evolutionary systems fit the bill. The local interactions of large numbers of
small components (i.e. genes) and feedback mechanisms (i.e. reproduction and
competition) result in structures at a higher level (i.e. the phenotype) that
would be difficult to explain via reductionism.
For
many emergence is the hallmark of complexity, and natural evolution is the
highest and best example of emergence. Exquisite forms such as butterfly wings,
leopards spots, the branching structures of trees, and spiral structures in
seed pods and flower petals, and indeed the entire realm of living things, seem
to offer “order for free” [4] as provisional end points in the long process of
evolution.
Philosophers
and theologians have argued that just as the complex design of a watch implies
the existence of an intelligent watchmaker, the infinitely more complex design
of the ecosystem and the plants and animals it contains implies the existence
of an infinite creator, which is to say God.
Emergence is offered by complexity science as a less mysterious, purely
mechanistic, explanation of creation.
But
even as such, emergent properties are often defined as “unexpected” or
“surprising” features that defy prediction or even understanding via dissection
into parts, and can only be appreciated in a holistic manner.
And
so it seemed with the solutions to the Traveling Salesman Problem. Upon completing the graphic shown above
(figure 1.1) I immediately decided to embark on a series of wall drawings or
murals. Each mural is site specific in
that a set of random points are generated to fit the specific shape of the
given wall. Then those points are
solved as a TSP problem and the resulting lines are painted and filled with
color.
I
expected that some would respond to these works in a way consistent with the
ironic social/political postmodern tone that remains dominant in the American
art world. After all, the traveling
salesman has an iconic status in American culture. Willie Loman in Arthur Miller’s play “Death of a Salesman”
epitomizes the hard working capitalist who ultimately fails because he views
the American dream as a purely material pursuit. And there is a tradition of bawdy “traveling salesman” jokes
where the eponymous anti-hero engages a sequence of farmer’s daughters or bored
housewives, often to no happy end. And
indeed one could observe that the same computing technology that allows us to
now solve large TSP’s has also, ironically enough, made traveling salesmen
increasingly irrelevant through the advent of web based marketing, video
conferencing, and so on.
But
such things were not my interest.
Artists often invent private languages, and just as felt and fat became
symbols for Joseph Beuys of his (possibly fictional) wartime experiences, for
me the Traveling Salesman Problem became a symbol of my experience with
emergence.
I made more TSP based designs and confirmed that they
shared a consistent aesthetic style. I continued to wonder how it was that a
genetic algorithm which solves the TSP, an exercise in optimizing a tour of
random points with no aesthetic agenda, and no feedback based on artistic judgment, could
generate murals with a consistent visual
style that
seemed anything but random.
2. TSP Solutions Considered Aesthetically and Mathematically
To
better understand the emergent form TSP solutions seem to exhibit I created 25
problems, each using 1000 points (cities) randomly distributed
within a circle. I distributed the points within
a circle to avoid any bias an aspect ratio or straight edges or corners might
introduce.
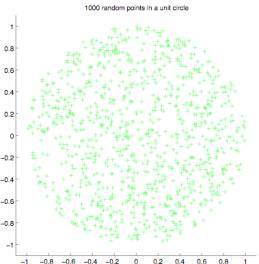
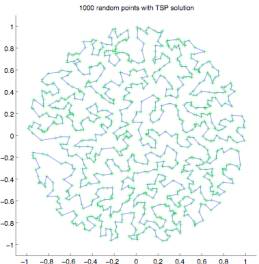
Figure 2.0
Figure 2.1

Figure
2.2
I
noted the following aesthetic factors that seemed to contribute to the style
these designs exhibit.
- Each design consists of
an enclosed area.
- Each design consists of
only one enclosed area. The border never crosses itself.
- There is ambiguity in
terms of figure and ground.
- The area seems to be
equally divided into figure and ground.
- The angles which make
up the borders seem evenly divided between convex and concave
- There is a relative lack
of extreme angles
I then embarked upon a modest
mathematical investigation of the apparently emergent form TSP solutions
exhibit considering each factor in turn.
2.1 Each design creates an enclosed area
It seems almost trivially obvious that any TSP solution is going to create an enclosed area. Imagine each city is a fence post and each city-to-city path taken is a barrier. If at a given point along the fence 2 persons would like to meet they may be tempted to walk to the next fence post. But at that post they will find another fence span blocking their meeting. And so they move on to the next fence post and find another span blocking their meeting. And so it goes until, by definition, the fence returns to the first fence post. Since the two people can never meet one of them must be trapped in an enclosed area.
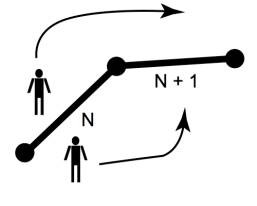
Figure
2.3
It’s
of course possible that the fence will cross itself, and when this happens it
creates two or more enclosed areas. But
this doesn’t seem to happen in TSP solutions.
Why might this be?
2.2 Each design creates only one enclosed area, i.e. the border never crosses itself
Consider the local situation where
a tour happens to cross itself. Four
cities (points) will be involved and we will ignore how those cities are
further connected to the overall tour.
In this situation there are only two ways to uncross the line
segments. Of these two ways one will
maintain the continuity of the tour, and the other will break the tour into two
smaller tours.
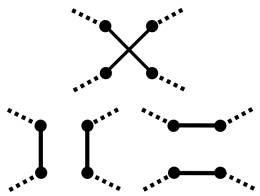
Figure
2.4
We now want to show that the total length of the two
crossed line segments is always greater than the total length of the uncrossed
line segments in both possible cases.
We will call the four cities in question A, B, C, and D. An additional point X is added at the point
of intersection.
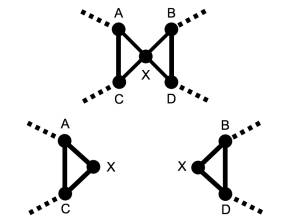
Figure
2.5
Since the shortest
distance between two points is a straight line, we can show:
AC < AX + XC
BD < BX + XD
AC + BD < (AX + XC) + (BX
+ XD)
AC + BD < (AX + XD) + (BX
+ XC)
AC + BD < AD + BC
In the same way
we can show that:
AB + CD < AD + BC
Having shown that the total length of the two crossed line segments is
always greater than the total length of the uncrossed line segments in both
possible cases, we can infer that any suggested solution that includes a pair
of crossed line segments can be improved by uncrossing those line
segments. Thus an optimal solution will
have no crossed line segments at all.
(Note though that it is quite possible that a solution with no crossed
line segments is still sub-optimal).
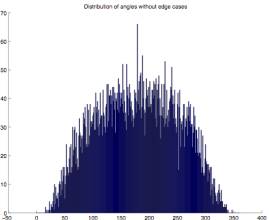
2.3 The angles which make up the borders seem evenly divided between convex and concave. There is a relative lack of extreme angles.
To verify this observation I did a
statistical analysis of the angles
contained in the 25 test problems. Even
though casual observation didn’t reveal any significant line segment length
relationships I also analyzed these. In
addition I did this for both all angles and line segments, and only those
angles and line segments within a .6 radius of the unit circle distribution. The latter was intended to eliminate any
possible edge effects.
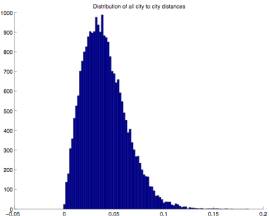
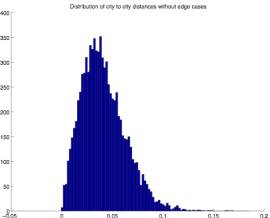
Figure 2.6 Figure
2.7
In this analysis
of all (Figure 2.6) and central (Figure 2.7) line segment lengths there is no
obvious edge effect. (The latter shows
greater variance, but this is to be expected due to the smaller sample
size). The distribution shows a unique
shape which no doubt contributes to the TSP solution’s visual signature. Both curves peak near .04. If 1000 points were uniformly distributed in
a unit circle using an optimal triangular mesh they would be at a distance of
about .06. It shouldn’t be too
surprising that distances in the TSP solution test cases are significantly less
than this because a random distribution will have tightly clustered points of
cities that can be exploited.
Figure 2.8 Figure
2.9
In this analysis
of all angles (Figure 2.6) and central angles (Figure 2.7), those that are less
than 180 degrees are convex edges of the enclosed figure, and those that are
greater than 180 degrees are concave edges.
Again there seems to be little edge effect. The overall distribution appears to be something other than
Gaussian. The curve is somewhat
flattened from 120 degrees to 240 degrees.
There is an apparent inflection point near 60 and 300 degrees where
extreme angles become quite rare. Both
distributions are very symmetric.
Figure
2.10
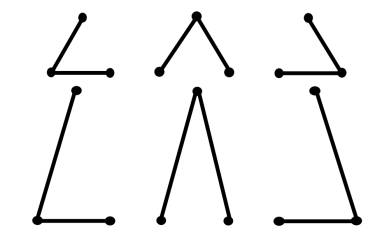
Figure 2.10
visually illustrates why angles less than 60 degrees are so rare. Three points
at 60 degree angles can be connected in a series in three different ways, and
all will result in the same total length.
But when one of the points is shifted further away to create a smaller
angle, that path quickly becomes the longest, and thus least optimal, option.
Aggregating the
angle statistics within each of the 25 test cases further confirms a relative
balance of convex versus concave edges.
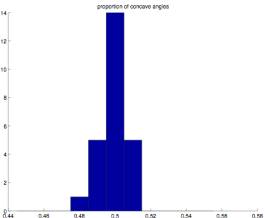
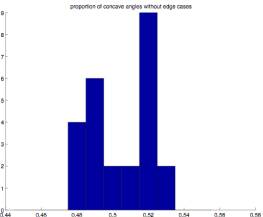
Figure 2.11 Figure 2.12
With only 25 test cases there is too much
variance to clearly exhibit a Gaussian distribution, especially where the edge
cases are eliminated, but the proportion of convex to concave angles is very
close to .5 in all cases. (All cases
are between .48 and .52).
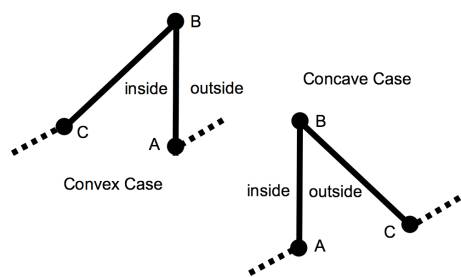
Figure 2.13
It makes perfect sense that
there is a balance of convex and concave contours. While some angles may be more likely than others, complementary
angles (as the distribution in figures 2.8 and 2.9 shows) are equally
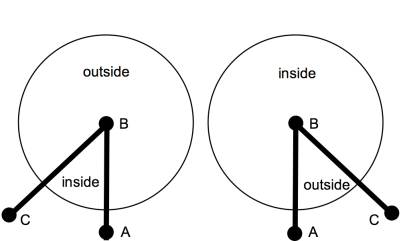
likely. Assume a tour is being
constructed and that points A and B have been connected. The inside of the soon-to-be enclosed space
is to the left and the outside is to the right. As a local phenomenon (figure 2.13) a third random point C to be
added to the tour is as likely to be on the left as the right. Thus adding a third point is as likely to
create a concave contour as a convex one.
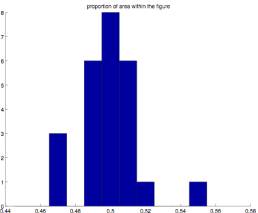
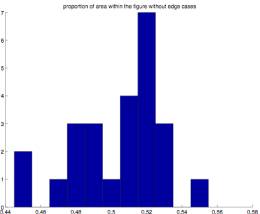
2.4 The area seems to be equally divided into figure and ground
Using Monte Carlo methods I
measured the amount of area captured by the enclosed figure versus the area
that remains on the outside. As shown
below (Figures 2.14 and 2.15), and allowing for the expected statistical
variation, the ratio of figure to ground is again very close to .5 for both the
entire figure and the portion of the figure with a radius of .6. (All cases are
between .45 and .55).
Figure 2.14 Figure 2.15
Similar
to the argument in the previous section, as a local phenomenon adding a third
point C as the tour is connected is as likely to add a lot as a little area in
the enclosed figure.
3. Emergence as a Philosophical Problem
Having completed this mathematical
consideration of TSP solutions, I still found the resulting graphics to be
formally satisfying, but strangely the phenomena no longer seemed to be
emergent.
It now felt as if these forms were
simply and exactly what they had to be. Each design consists of an enclosed
area because any connected loop of nodes would have to. Each design consists of only a single
enclosed area because, as we have seen, designs that create multiple enclosed
areas are suboptimal solutions. The
ambiguity of figure and ground is caused by the equal distribution of angles,
the equal distribution of convex and concave contours, and the even
distribution of area within and without the figure. All of this is due to the probabilistic symmetry of randomly
placed cities. The limited number of
very small and large angles is due to the cost in trip length such angles
exact. The mean length of the line
segments is not surprising when considered in the context of the separation
lengths required to create a uniform grid of an equal number of cities.
Somehow improved
understanding had evaporated the sense of emergence.
Although many scientists seem very
comfortable in referring to various complexity related properties as being
emergent, the concept of emergence is a thorny philosophical problem that
predates current thinking about complex
systems.
One has to wonder whether emergence is in the eye of the beholder. Could it be that Marvin Minsky is correct
when he refers to emergence as a “suitcase concept’ we use to deceive ourselves
by filling it with “things we don’t understand yet”? [5] Might it be that
extraterrestrial beings endowed with an advanced intelligence wouldn’t consider
the evolution of earthly plants and animals as emergence, but would simply view
it on a par with other non-emergent phenomena?
Often emergence is casually defined
relative to the appearance of “surprising” or “unpredictable” features not
present in a systems components, or with a slogan such as “the whole is greater
than the sum of its parts”. But does
that endow emergence with ontological integrity? Is emergence real, or is it
merely an epistemological consideration that says more about human consciousness
than external reality?
But further, if emergence is merely an experience without any specific
basis in the physical world, does that mean it isn’t real? Following John Searle’s thoughts on
consciousness [6], perhaps emergence like other qualia is real but partitioned
into the realm of what he calls “first person ontology”.
Emergence as a philosophical problem remains an open question. But this
actually increases my enthusiasm for this series of murals. Often an artists role, and the private
language he or she may develop, is more about asking important questions than
providing pat answers. In addition I
hope the Traveling Salesman series can serve as an example of how the
exploration of systems through generative art can act as a sort of experimental
philosophy. I remain convinced that
even in these postmodern times philosophy can be pursued via artistic
experimentation.
References
[1] Galanter, P. Foundations
of generative art systems – a hybrid survey and studio class for graduate
students. Generative Art 2001: Proceedings of the 4th
International Conference. Generative Design Lab, Milan Polytechnic, Milan 2001
[2] Fogel, L. J. (1999). Intelligence
through simulated evolution : forty years of evolutionary programming. New
York, Wiley.
[3]
http://www.tsp.gatech.edu/
[4] Kauffman,
S. A. (1995). At home in the universe : the search for laws of
self-organization and complexity. New York, Oxford University Press.
[5] In a talk presented at the 2003 International Conference on Complexity Science,
Nashua New NH
[6] Searle, J. R. (1997).
The Mystery of Consciousness, New York, New York Review of Books