The Development of a Tool for the Preference Assessment of the Visual Aesthetics of an Object Using Interactive Genetic Algorithms

Jarod Kelly, Ph.D. Student

e-mail: jckelly@umich.edu

Prof. Panos Papalambros, Ph.D.

e-mail: pyp@umich.edu

Department of Mechanical Engineering, University of Michigan, Ann Arbor, MI, USA.

Prof. Gregory Wakefield, Ph.D.

e-mail: ghw@umich.edu

Department of Electrical Engineering and Computer Science, University of Michigan, Ann Arbor, MI, USA.

Abstract

Interactive evolutionary algorithms (IEAs) have been proposed as creativity aids to designers with regard to visual aesthetics. Algorithms have been developed to expose the designer to new designs and thus spark imagination and improve creativity. The present paper focuses on utilizing interactive genetic algorithms (IGAs), a subset of IEAs, to understand the visual aesthetic preferences of the user. A design concept is input to the IGA program, which utilizes information gathered from the user to create new designs. The program collects preferences from the user in a simulated “marketplace” setting. These preferences inform the evolution of the object’s design over several generations until a final “ideal design" is reached. This "ideal design" is considered to be the most preferred visual aesthetics for that user within the specified design space. Monte Carlo simulations indicate that the IGA can locate such ideal designs with high probability. Human studies suggest that users can express their visual aesthetic preferences for a design with the IGA. This is important because few scientific tools exist for acquiring such preference information reliably and efficiently. Design decisions regarding visual aesthetics of a product often interact with its technical attributes. The proposed preference assessment tool aims to facilitate such interactions in a more analytical manner than is currently available.

Introduction

Product design aims to create artifacts that meet or exceed users’ wants and needs. Metrics that govern how well a designer meets those wants and needs are often amorphous but can gain clarity within certain domains of design. Visual aesthetics are much more difficult to quantify than technical performance. This paper proposes a method for eliciting visual aesthetic preferences from the user.

Interactive genetic algorithms (IGAs) are built upon the foundations of evolutionary computing, specifically, the genetic algorithm (GA) introduced by Holland in 1975 [1]. IGAs work similarly to GAs with the important difference that the fitness of members in the IGA population is evaluated by a human and not by a mathematical function. This allows a human user to interact with the genetic instantiations of a potential design so as to influence the evolution of a population of designs to fit his or her preferences. In the current paper we utilize the evolutionary process to elicit user preferences. Simply asking what one wants is insufficient. Providing options and asking for selections will allow users to actually evaluate whether or not they like an object. Repeating this process with continually informed, updated and personally tailored sets of choices allows a user to hone in on a design that is truly preferred. Assuming that the end user of an object is the final arbiter of the object’s visual aesthetics, the proposed method should assist in discovering what these aesthetic preferences may be and use them in the design of products for the marketplace.

The paper is organized as follows. We discuss the current practice of preference assessment and the foundations of IGA, followed by an explanation of the algorithm we propose and its interface for the user. Finally, we describe two experiments that better help us understand the role of IGA-related parameters, and to validate the method as a tool for assessing user preference.

Background

Marketers and psychologists use several techniques for preference assessment ranging from focus groups to scientifically developed mathematical models of consumer choice. In the present context, the most interesting techniques are those that yield preference maps, or models, such as conjoint analysis, MDPREF, and PREMAP. After examining these, we describe IGAs.

Conjoint analysis is used extensively in the social science and marketing communities to determine the ideal combination of feature attributes based on the preference responses of a test subject or group. It has been frequently used within industry to determine information related to product design, concept evaluation, product positioning, and market segmentation [2]. The method assumes that consumers attempt to maximize their utility when they make choices. In order to collect data for a conjoint analysis, respondents are shown several potential products, descriptions of products, or images of products. Each product is similar in nature, but the levels of the product attributes are varied. Respondents are then asked to evaluate the products in some fashion. The responses provide data for model regression. However, it becomes increasingly difficult to conduct conjoint analysis as the number of attributes and their associated levels increase due to the increasing number of responses required of a subject. Thus far, no literature is available that describes efforts to quantify visual aesthetics using conjoint analysis, and it is possible that such efforts may be clouded by nonlinear effects associated with preference and visual aesthetics.

Multidimensional analysis of preference data (MDPREF) developed by Chang and Carroll [3] uses data obtained through a survey to generate an internal mapping of preference. Only information collected in the MDPREF query is used for interpretation, thus there are no inherent scales on which the data can be explicitly analyzed, but the configuration and segmentation of the data can be useful [4-5]. Input data consist of an average attribute-by-objects matrix. Average preference evaluations are obtained through compilation of several surveys regarding the proposed attributes and objects [3]. Each attribute is represented as a vector, and each object is plotted as a point on a map in an m-dimensional space. The resulting figure contains descriptive perceptual axes (the attribute vectors) and is populated with points (objects), appropriately positioned within the vector space. By relating each object to each vector we can get a sense of how each particular attribute contributes to the object’s preference. MDPREF is based on a linearized model such that preference increases along each attribute vector towards infinity. Thus, the distance between an object's projection onto an attributes vector and the origin varies directly with preference. MDPREF can be a useful tool in gaining preference information related to product design. However, it does not provide enough information to create a map of the design space that could be used for engineering design because it is based on linearized models and has no direct correlation to engineering quantities. The primary benefit of MDPREF is that it is informative: It can show how one product is perceived to relate to another with respect to a variety of attributes. While this type of analysis is useful in understanding market preferences for certain product offerings (or even aesthetic features if described properly), it lacks the desired fidelity for creating a useful preference map in the desired scenario [4].

PREFMAP, also developed by Chang and Carroll [6], relates a stimulus space to preference data in order to generate an external mapping of preference. In an external mapping of preference, the stimulus space is based on data obtained independently of the preference assessment [4, 6]. For instance, if several examples of light were shown to subjects and they rated their preference for each sample, then we could determine preference for brightness by mapping the light samples' preference onto a stimulus space of lumens. The evaluated data that is input to PREFMAP is a subjective ranking by a subject of his or her preferences for certain stimuli (variations on a particular design, for example). PREFMAP has four different phases of analysis associated with four different types of regression models. Three of these models, phases I through III, are based on an ideal point concept, while phase IV is a vector model of preference. The basic idea behind PREFMAP is an axiomatic assumption that each individual has an ideal point of maximum preference and is capable of ranking different stimuli in such a way that the ideal point is revealed [4]. Recent investigations by Petiot and Chablat [7] used a variation on PREFMAP to study a user's aesthetic preference for a table glass shape; however, they linearized their final results, thus suggesting that preference was met at the bounds of their design space.

IGAs have been used for a variety of purposes, but most often they attempt to utilize human knowledge and experience to either provide personalized tuning, or to avoid the use of computationally expensive (or impossible) design evaluations [8-11]. IGAs were first investigated by Dawkins to explore the use of guided evolutionary design to create bi-morph, or treelike, structures [12]. IGAs, similar to GAs, describe a design using several variables and parameters (variables can change, parameters are fixed). The variables are arranged in a chromosome structure (often binary) and many individuals (or genotypes) are created from this chromosome. This is analogous to biology in which all humans have essentially the same genetic chromosome, but each person has a distinct genotype. To begin either an IGA or GA evaluation, an initial population of individuals is created. Next, the individuals within this population are evaluated based on some criteria. For GAs a mathematical fitness function is used to evaluate the fitness of the individuals, and populations are often very large. For IGAs, a human provides an evaluation of the population; these populations are typically orders of magnitude smaller than those of GAs. From the evaluation, the algorithm determines parents which are used to create a new population of children through crossover and mutation. The parents of a child are selected based upon typically probabilistic criteria, in which individuals that have high fitness evaluations are more likely to be chosen as parents than those that have low evaluations. Once selected, parents exchange complementary genetic material through crossover to create a child. This genetic material is then altered, in a random fashion, by a mutation, which causes one bit of the binary genetic structure to change. Crossover is important because it allows ‘fit’ parents to ‘mate’, and hopefully create better children. Mutation is important as it allows the possibility for exploration of new and potentially better designs that would be unattained through crossover alone. This process of generational evaluation and repopulation is repeated several times until some stopping criterion is met. For IGAs, this stopping criterion is often a specific number of generations.

The difference between using IGAs to inspire a designer and using it to understand the wants of the user is that the former presupposes abundant designer intuition, whereas the latter assumes that the user is capable of expressing his preferences through selection. In IGA implementations that serve as inspirational design tools, a high level of mutation is utilized in order to expose the designer to very unique, unanticipated designs. It is expected that the large variety of design options will enhance the creativity of the designer [13]. In contrast, an IGA that seeks to understand the preferences of an individual must converge as generations progress. This convergence is required as it shows both stability and uniqueness in the selections of the individual.

Previous IGA investigations for the discovery of design preference include visual systems but contain little evidence that the intended design is found as a result of the IGA process [8,9,13]. Several audio-based IGAs have been proposed and validated in determining effective tuning for very personalized devices, such as hearing aides [10]. A properly designed IGA should converge to a user-preferred design. In this paper we attempt to validate this convergence using a pairwise comparison study following the IGA survey.

The IGA Algorithm

The proposed IGA strategy is demonstrated using a specific object: a cola bottle. In this section we describe algorithmic details and the graphical user interface (GUI) for the user’s input evaluation.

Chromosome

The design space for the cola bottle is composed of two variables and three (fixed-value) parameters that represent points on the bottle’s surface. A spline fit through the five points creates unique bottle shapes. Figure 7 shows this representation with variables, R2 and R4, and parameters, R1, R3, R5. All points are fixed vertically, and R2, R4 can vary radially. Variable representation is based on a natural binary coding scheme, coded as a four-bit number, each with 16 discrete levels, leading to a total of 256 distinct bottle shapes.

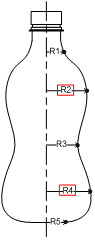
Figure 7: The cola bottle design chromosome is contians points R2 and R4 as variables.

Selection and Internal Mechanics

In each evaluation cycle, the user is presented with the entire population of 16 individuals, to simulate the type of decision a user would face in a store. During the first seven generations of the IGA, the user is asked to select the four most preferred bottle designs, and pick only one in the final generation. This process agrees with reports by other researchers, which suggest that ranking each item within the population (a common IGA method) becomes tedious and fatigues the respondent [8-11,]. The whole population is then submitted to a roulette-wheel parent-selection process. Highly preferred individuals are each given a 22.5% chance of selection while unselected individuals are given a 0.83% chance. Each combination of parents produces a single offspring; however no parent is ever expunged from the roulette selection-process. Consequently, a parent can create multiple children and even mate with itself. Single-point crossover is used for the creation of new children. For mutation, a design space mutation operator is employed as opposed to the standard bit-space mutation operator. This design space operator (randomly applied) manipulates a single variable of a child to increase or decrease a single unit in the design space as indicated in Figure 8. Monte Carlo investigations using a predefined search agent suggest that this design space operator is much more effective at achieving the most preferred design than the bit space mutation operator, and that the mutation rate should be ~50%.

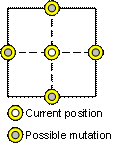
Figure 8: The design space operator causes the design variable to change by one unit.

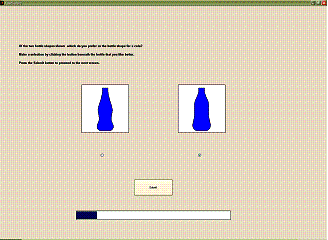
Graphical User Interface

The GUI is shown in Figure 9. Each individual (product design) is randomly placed within the selection matrix, except for the first population. Each user sees the exact same first population of shapes; it is a set of shapes that spans the entire design space. Following that, each user defines the new populations through his or her choices, and the following populations are all randomly placed within the selection matrix. This type of matrix was chosen to be similar to a store shelf where one might actually make this type of choice. The user selects (or unselects) their favourite shapes using a mouse, and submits those choices via a ‘Submit’ button on the right of the screen. The screen visually informs the user of how many selections they have made and how many generations remain to be completed. Following completion of this task the user is explicitly asked if he is satisfied with the final choice.

Figure 9: The GUI for the IGA allows the user to make selections.

In a follow-up study, the users are asked to make pairwise comparisons between their final selection of the IGA and several other options. This GUI is shown in Figure 10. The user is presented with 15 comparisons; seven of these comparisons contain the subject’s final IGA shape selection. These seven questions are randomized within the 15 questions and the final shape is randomly placed on the left or right of the screen. The user is asked to select one of two options shown. Notably, a predefined shape-finding task is placed between the preference IGA and the pairwise comparison tasks. This task is to use the IGA to find a circle and is conducted in this order to prevent the user from remembering her final selection from the preference task. Using these data, we can examine the choice proportion between the final selection from the IGA and the items that it was paired against in order to validate the IGA as an effective preference assessment tool.

Figure 10: In the pairwise comparison survey users select their most preferred of two options.

IGA Validation

Two studies were conducted to show that the IGA can assess preference. First, an autonomous agent was used to evaluate populations and make selections in an attempt to find that agent’s ‘favourite’ design. Monte Carlo simulations were conducted using several IGA parameter settings for mutation rate, mutation type, number of selections, and roulette percentage. Second, using the insights of the Monte Carlo simulation, human studies were conducted to investigate the ability of users to find a predefined shape and a highly preferred soda bottle shape. The term ‘highly preferred’ is used because even when using GAs with a mathematically defined fitness function we cannot guarantee that the final design will be optimal. GAs do guarantee that a ‘good’ solution will be found [14].

Monte Carlo Simulation

A Monte Carlo simulation was conducted using a computer agent to determine effective tuning parameters for the IGA. The agent proceeded through the IGA process as a human respondent would, selecting a specified number of shapes in each generation and only one in the final population. Actually, the agent evaluated each member of the population to find the designs with the shortest Euclidean distance between themselves and a ‘goal’ design. This goal design was a randomly generated string of eight bits, thus no preference was given to any particular schema (or collection of bit strings). The simulation was run 10,000 times for each of the tuning parameters; these were the number of selections a user could make (between 2 and 4), the percentage of the roulette wheel allocated to selected individuals, and the mutation rate (which varied between 60% and 0%).

Figure 11 shows that the design space mutation operator outperforms the bit space mutation operator in its ability to obtain the pre-defined ideal solution in the agent- based Monte Carlo simulation. It also indicates that a high rate of mutation, roughly 50%, works well for this given type of mutation operator. The figure also suggests that a high roulette percentage is desirable. Note that four selections are used in this study; analysis of the data indicates that the number of choices a user made only impacted the agent’s ability to obtain the ideal design if roulette percentage was below 70%. Thus, we use the design space mutation operator with a 50% chance of mutation, a roulette wheel setting of 90% and a generational selection of four. The roulette wheel setting is not 100% because we believe that, unlike an agent, humans will not make mathematically defined decisions, but idiosyncratic ones. So, it is important that some variety exists in the generations. A 100% roulette setting would significantly decrease the amount of variety that a person would observe during the course of the IGA. Figure 12 shows the effect of applying these settings within the Monte Carlo simulation. Notice that the agent-based search converges toward the ideal design, while a random search does not converge to the ideal design.

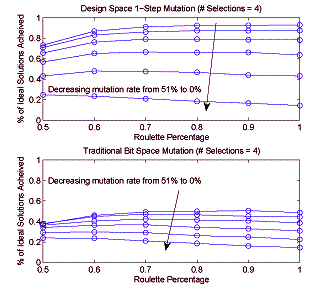
Figure 11: Design space mutation operator compared to bit space mutation operator.

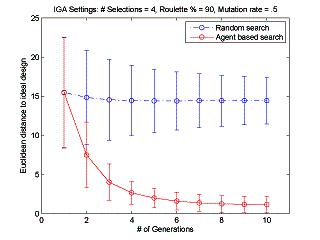
Figure 12: Agent based search versus random search using given IGA settings.

Human User Studies

Human subject studies were conducted to validate the IGA’s ability to allow users to (i) obtain a pre-defined shape and (ii) express their preference through the object selection process. In the first study we asked users to use the IGA to find a circle; in the second to express preference for a cola bottle shape This study is still in progress but initial results indicate that the IGA tool is indeed capable of achieving both goals.

In the predefined shape study 83.3% of the 12 subjects explicitly found the circle using the IGA tool. Of the remaining 16.7%, the average of the Euclidean distance away from the intended shape was .21. This is just over 2 discrete units within the design space. Further, a ‘satisfaction’ question was posed to the users after completion of the final IGA selection to ascertain whether or not they believed that they found the circle or not, and 100% of the population indicated that they had found the desired shape. These results suggest that human evaluation may be utilized as a “black box” function within the visual IGA and that a highly preferred design, not known a priori, may be discovered.

For the study of preference assessment, 100% of 12 subjects stated that they found the design they intended with their final selection of the IGA. This indicates that the user was personally satisfied with and accepting of the final shape selected in the IGA. In the pairwise comparison study 90.5% of the highly preferred IGA shapes were selected over the other presented options. This gives added credibility to the usefulness of the IGA as a preference assessment tool, and it is more convincing than the satisfaction question.

Conclusions

The IGA developed here shows promise in its ability to help obtain useful information regarding aesthetic preference. This information is gathered through the interactive process of user selection and computational adjustment of posed choices. Monte Carlo simulations provide an effective means of tuning the parameters within the IGA, such that human users would be likely to find a goal design. This goal-seeking ability was validated through user studies. The ability to illuminate a highly preferred design for the user was also validated using self-reporting and pairwise-comparison methods. The IGA can be quickly adjusted to allow investigation of different shapes that are defined by a greater number of variables. Thus, a flexible tool is offered to designers to obtain valuable information on user aesthetic preferences for specific objects.

Bibliography

[1] Holland, J.H. 1975. Adaptation in Natural and Artificial System. Ann Arbor, Michigan, USA: The University of Michigan Press.

[2] Green, P. E., & Srinivasan, V. 1990. “Conjoint Analysis in Marketing: New Developments with Implications for Research and Practice”. Journal of Marketing, 54(4), 3-19.

[3] Chang, J. J., & Carroll, J. D. 1969. How to use MDPREF, a computer program for multidimensional analysis of preference data. Bell Telephone Laboratories, Murray Hill, MJ.

[4] Coxon, A. P. M., Jackson, J. E., Davies, P. M., Smith, H. V., Sachs, L., & Schmee, J. 1985. “The Users Guide to Multidimensional Scaling”. TECHNOMETRICS, 27(1).

[5] Young, N. D., Drake, M., Lopetcharat, K., & McDaniel, M. R. 2004. “Preference mapping of Cheddar cheese with varying maturity levels”. Journal of dairy science, 87(1), 11-19.

[6] Chang, J. J., & Carroll, J. D. 1972. How to use PREFMAP and PREFMAP-2: Programs which relate preference data to multidimensional scaling solutions. Unpublished manuscript, Bell Telephone Labs, Murray Hill, NJ.

[7] Petiot, J. F., & Chablat, D. 2003 (November 5-7, 2003). “Subjective Evaluation of Forms in an Immersive Environment”. In: Proceedings of Virtual Concept - 2003.

[8] Cho, S.B. 2002. Towards creative evolutionary systems with interactive genetic algorithm. Applied Intelligence: The International Journal of Artificial Intelligence, Neural Networks, and Complex Problem-Solving Technologies, 16(2), 129{38.

[9] Nishino, H., Takagi, H., Cho, S.B., & Utsumiya, K. 2001. “A 3D modelling system for creative design”. Pages 479-86 of: Proceedings of 15th International Conference on Information Networking, 31 Jan.-2 Feb. 2001.

[10] Durant, E.A., Wakefield, G.H., Van Tasell, D.J., & Rickert, M.E. 2004. “Efficient Perceptual Tuning of Hearing Aids With Genetic Algorithms”. IEEE Transactions on Speech and Audio Processing, 12(2), 144-155.

[11] Kamalian, R., Zhang, Y., Takagi, H., & Agogino, A. M. 2005. “Reduced Human Fatigue Interactive Evolutionary Computation for Micromachine Design”. Proceedings of 2005 International Conference on Machine Learning and Cybernetics.

[12] Dawkins, R. 1986. The blind watchmaker. Harlow : Longman Scientific and Technical.

[13] Smyth, S. N., & Wallace, D. R. 2000. “Towards the synthesis of aesthetic product form”. Proc.DETC2000/DTM-14554, ASME, New York.

[14] Whitley, L. D. 2001. “An overview of evolutionary algorithms: practical issues and common pitfalls”. Information Software Technology, 43(14), 817{831.